题目内容
18.学校计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑比购买4台学习机多200元,购买2台平板电脑和3台学习机共需8100元.(1)求购买1台平板电脑和1台学习机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过166600元,且购买学习机的台数不超过购买平板电脑台数的1.5倍.请问有哪几种购买方案?哪种方案最省钱?
分析 (1)设购买1台平板电脑和1台学习机各需x元,y元,根据题意列出方程组,求出方程组的解得到x与y的值,即可得到结果;
(2)设购买平板电脑x台,学习机(100-x)台,根据“购买的总费用不超过166600元,且购买学习机的台数不超过购买平板电脑台数的1.5倍”列出不等式组,求出不等式组的解集,即可得出购买方案,进而得出最省钱的方案.
解答 解:(1)设购买1台平板电脑和1台学习机各需x元,y元,根据题意得:
$\left\{\begin{array}{l}{x-4y=200}\\{2x+3y=8100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3000}\\{y=700}\end{array}\right.$,
答:购买1台平板电脑和1台学习机各需3000元和700元;
(2)设购买平板电脑x台,学习机(100-x)台,
根据题意得:$\left\{\begin{array}{l}{100-x≤1.5x}\\{3000x+700(100-x)≤166600}\end{array}\right.$,
解得:40≤x≤42,
∵x只能取正整数,
∴x=40,41,42,
当x=40时,y=60;x=41时,y=59;x=42时,y=58;
方案1:购买平板电脑40台,学习机60台,费用为120000+42000=162000(元);
方案2:购买平板电脑41台,学习机59台,费用为123000+41300=164300(元);
方案3:购买平板电脑42台,学习机58台,费用为126000+40600=166600(元),
则方案1最省钱.
点评 此题考查了一元一次不等式组的应用和二元一次方程组的应用,读懂题意,找出题中的等量关系,列出方程组和不等式组是解本题的关键.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案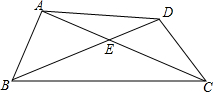 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=$\sqrt{2}$,BE=2$\sqrt{2}$.
如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=$\sqrt{2}$,BE=2$\sqrt{2}$.
 如图是在方格纸上画出的小旗图案,若用(1,1)表示点A,(1,5)表示点B,(2,3)表示点D,那么点C的位置可表示为(4,3).
如图是在方格纸上画出的小旗图案,若用(1,1)表示点A,(1,5)表示点B,(2,3)表示点D,那么点C的位置可表示为(4,3).