题目内容
已知等腰直角三角形ABC的腰长为4,半圆的直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,则半圆的半径为 .
考点:切线的性质,等腰直角三角形
专题:
分析:有两种情况:①是直径在斜边上,首先连接OD,由切线的性质,易得OD⊥AB,即可得OD是△ABC的中位线,继而求得OD的长.②是直径在腰上,首先连接OD,由切线的性质,易得OD⊥BC,即可根据勾股定理求得OD的长.
解答: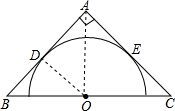 解:①∵半圆的直径在△ABC的斜边上,且半圆的弧与△ABC的两腰相切,切点为D、E,
解:①∵半圆的直径在△ABC的斜边上,且半圆的弧与△ABC的两腰相切,切点为D、E,
如图,连接OD,OA,
∵AB与⊙O相切,
∴OD⊥AB,
∵在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,
∴AO⊥BC,
∴OD∥AC,
∵O为BC的中点,
∴OD=
AC=2.
②∵半圆的直径在△ABC的腰上,且半圆的弧与△ABC的斜边相切,切点为D,
如图2,连接OD,设半圆的半径为r,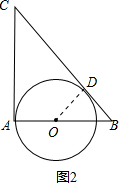
∴OB=4-r,
∵在等腰直角三角形ABC中,AB=AC=4,
∴∠B=45°,
∴△OBD是等腰直角三角形,
∴OD=BD=r,
∴2r2=(4-r)2,解得r=-4+4
,r=-4-4
(舍去),
故答案为2或-4+4
.
 解:①∵半圆的直径在△ABC的斜边上,且半圆的弧与△ABC的两腰相切,切点为D、E,
解:①∵半圆的直径在△ABC的斜边上,且半圆的弧与△ABC的两腰相切,切点为D、E,如图,连接OD,OA,
∵AB与⊙O相切,
∴OD⊥AB,
∵在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,
∴AO⊥BC,
∴OD∥AC,
∵O为BC的中点,
∴OD=
| 1 |
| 2 |
②∵半圆的直径在△ABC的腰上,且半圆的弧与△ABC的斜边相切,切点为D,
如图2,连接OD,设半圆的半径为r,

∴OB=4-r,
∵在等腰直角三角形ABC中,AB=AC=4,
∴∠B=45°,
∴△OBD是等腰直角三角形,
∴OD=BD=r,
∴2r2=(4-r)2,解得r=-4+4
| 2 |
| 2 |
故答案为2或-4+4
| 2 |
点评:此题考查了切线的性质、切线长定理以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
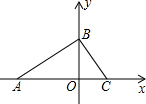 已知:如图,在平面直角坐标系中,点A,B分别在x,y轴上,且OA,OB的长(OA>OB)是一元二次方程x2-7x+12=0的两根.
已知:如图,在平面直角坐标系中,点A,B分别在x,y轴上,且OA,OB的长(OA>OB)是一元二次方程x2-7x+12=0的两根.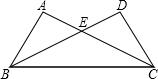 如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.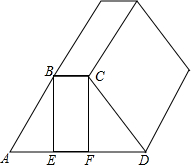 梯形ABCD是一段公路路基的截面图,现在需要在2个斜坡面植草,已知∠A=45°,DE=8m,DF=6m,路基长30m,每平方米的草坪的费用为a元,求2个斜坡面植草的总费用.
梯形ABCD是一段公路路基的截面图,现在需要在2个斜坡面植草,已知∠A=45°,DE=8m,DF=6m,路基长30m,每平方米的草坪的费用为a元,求2个斜坡面植草的总费用.