题目内容
 A,B,C三个村庄在一条东西走向的公路沿线,如图,AB=2km,BC=3km,在B村的正北方向有一个D村,测得∠ADC=45°.今将△ACD区域规划为开发区,除其中4km2的水塘外,均作为建筑或绿化用地,试求这个开发区的建筑及绿化用地的面积是多少?
A,B,C三个村庄在一条东西走向的公路沿线,如图,AB=2km,BC=3km,在B村的正北方向有一个D村,测得∠ADC=45°.今将△ACD区域规划为开发区,除其中4km2的水塘外,均作为建筑或绿化用地,试求这个开发区的建筑及绿化用地的面积是多少?考点:勾股定理的应用
专题:
分析:将△ABD,△BCD以DA,DC作轴对称变换,得△AFD,△ECD,延长EC,FA交于点G,易证四边形DFGE是正方形,设BD=x,利用勾股定理建立方程求出x的值,进而求出三角形,所以这个开发区的建筑及绿化用地的面积也可求出.
解答: 解:如图所示:将△ABD,△BCD以DA,DCBD作轴对称变换,得△AFD,△ECD,延长EC,FA交于点G,
解:如图所示:将△ABD,△BCD以DA,DCBD作轴对称变换,得△AFD,△ECD,延长EC,FA交于点G,
∴四边形DFGE是正方形,设BD=x,
在RT△AGC中有AC2=AG2+CG2
即25=(x-2)2+(x-3)2
解得x=6,
∴S△ADC=
×AC•DB=15km2,
∴开发区的建筑及绿化用地的面积是15-4=11 km2
 解:如图所示:将△ABD,△BCD以DA,DCBD作轴对称变换,得△AFD,△ECD,延长EC,FA交于点G,
解:如图所示:将△ABD,△BCD以DA,DCBD作轴对称变换,得△AFD,△ECD,延长EC,FA交于点G,∴四边形DFGE是正方形,设BD=x,
在RT△AGC中有AC2=AG2+CG2
即25=(x-2)2+(x-3)2
解得x=6,
∴S△ADC=
| 1 |
| 2 |
∴开发区的建筑及绿化用地的面积是15-4=11 km2
点评:本题考查了勾股定理的应用、正方形的面积公式、三角形的面积公式、轴对称图形的性质,题目的设计新颖,难度较大,是一道不错的中考题.

练习册系列答案
相关题目
关于近似数1.6万,下列说法正确的是( )
| A、精确到十分位 |
| B、精确到万位 |
| C、精确到个位 |
| D、精确到千位 |
在(x+2y-2z)(x-2y+z)=[x+2□][x-□]的□中填入的代数式分别是( )
| A、y-2z,2y-z |
| B、y-z,2y+z |
| C、y-z,2y-z |
| D、y-2z,2y+z |
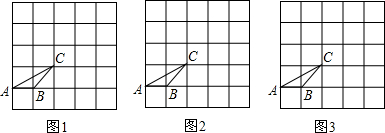
 如图,方格纸中小正方形的边长都为1,A、B、C在小正方形顶点上.
如图,方格纸中小正方形的边长都为1,A、B、C在小正方形顶点上.