题目内容
19．
如图，已知点C（0，2），D（4，2），F（4，0），请限用无刻度的直尺作出下列抛物线的顶点P．
分析 根据二次函数图象的性质，二次函数图象关于对称轴对称，可以分别作出图中两个抛物线的对称轴，本题得以解决．
解答 
解：抛物线与x轴交于点A、B，由抛物线的对称性可知四边形OCDF是矩形，四边形ABDC是等腰梯形，抛物线的对称轴经过矩形OCDF和等腰梯形ABDC的中点．
连接OD、CF，交于点O1，连接AD、BC交于点O2，再连接O1O2，则O1O2与抛物线的交点为抛物线的定点P．如图所示．
点评 本题考查二次函数的性质，解题的关键是明确二次函数的性质，二次函数的图象具有对称性．
练习册系列答案
阅读快车系列答案
相关题目
7．
如图，在△ABC中，D、E分别是AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数是（ ）
如图，在△ABC中，D、E分别是AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数是（ ）| A． | 15° | B． | 20° | C． | 25° | D． | 30° |
4．
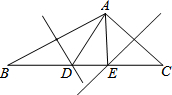如图，△ABC中，∠BAC＞90°，其中AB、AC的垂直平分线交BC于点D、E，△ADE的周长为16，则BC的长（ ）
如图，△ABC中，∠BAC＞90°，其中AB、AC的垂直平分线交BC于点D、E，△ADE的周长为16，则BC的长（ ）| A． | 16 | B． | 18 | C． | 24 | D． | 32 |
8．下列等式一定成立的是（ ）
| A． | $\sqrt{5}-\sqrt{2}=\sqrt{3}$ | B． | $\frac{{\sqrt{7}}}{{\sqrt{5}}}=\sqrt{\frac{7}{5}}$ | C． | $\sqrt{x^2}=\sqrt{x}•\sqrt{x}$ | D． | $\sqrt{{{（π-4）}^2}}$=π-4 |