题目内容
(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图中对顶角和邻补角的个数
(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图中对顶角和邻补角的个数
(3)依此类推,n条直线相交,最少有 个交点,最多有 个交点,对顶角有 对,邻补角有 对.
(2)四条直线相交,最少有
(3)依此类推,n条直线相交,最少有
考点:相交线,对顶角、邻补角
专题:规律型
分析:当直线同交于一点时,只有一个交点;当直线两两相交,且不过同一点时,交点个数最多;根据对顶角与邻补角的定义找出即可.
解答:解:(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
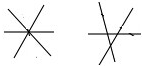
对顶角:6对,邻补角:12对;
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
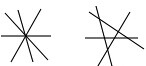
对顶角:12对,邻补角:24对;
(3)n条直线相交,最少有1个交点,最多有
个交点,对顶角有4n对,邻补角有2n对.
故答案为:(1)1,3;(2)1,6;(3)1,
,4n,2n.
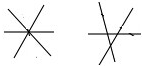
对顶角:6对,邻补角:12对;
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:

对顶角:12对,邻补角:24对;
(3)n条直线相交,最少有1个交点,最多有
| n(n-1) |
| 2 |
故答案为:(1)1,3;(2)1,6;(3)1,
| n(n-1) |
| 2 |
点评:本题考查了直线两两相交时交点的情况,以及对顶角与邻补角的定义,关键是画出图形.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由. 如图,AB=BC=CA=AD,则∠BDC=
如图,AB=BC=CA=AD,则∠BDC=