题目内容
因式分解：
（1）（2x+y）2+2y（2x+y）+y2；
（2）2ax5-8ax；
（3）（3x+y）2-（x+3y）2．
（1）（2x+y）2+2y（2x+y）+y2；
（2）2ax5-8ax；
（3）（3x+y）2-（x+3y）2．
考点：提公因式法与公式法的综合运用
专题：
分析：（1）直接利用完全平方公式分解因式得出即可；
（2）首先提取公因式2xa，进而利用平方差公式分解因式得出即可；
（3）直接利用平方差公式分解因式得出即可．
（2）首先提取公因式2xa，进而利用平方差公式分解因式得出即可；
（3）直接利用平方差公式分解因式得出即可．
解答：解：（1）（2x+y）2+2y（2x+y）+y2
=（2x+y+y）2
=4（x+y）2；
（2）2ax5-8ax
=2ax（x4-4）
=2ax（x2+2）（x2-2）；
（3）（3x+y）2-（x+3y）2．
=（3x+y+x+3y）（3x+y-x-3y）
=（4x+4y）（2x-2y）
=8（x+y）（x-y）．
=（2x+y+y）2
=4（x+y）2；
（2）2ax5-8ax
=2ax（x4-4）
=2ax（x2+2）（x2-2）；
（3）（3x+y）2-（x+3y）2．
=（3x+y+x+3y）（3x+y-x-3y）
=（4x+4y）（2x-2y）
=8（x+y）（x-y）．
点评：此题主要考查了公式法分解因式，熟练应用乘法公式分解因式是解题关键．
练习册系列答案
相关题目
如图，OA⊥OB、OC⊥OD，则∠l与∠2的大小关系是（ ）| A、∠1＞∠2 |
| B、∠l=∠2 |
| C、∠l＜∠2 |
| D、以上都不对 |
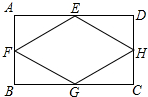如图，E、F、G、H分别是矩形ABCD四边AB、BC、CD、AD的中点，