题目内容
观察下表:
我们把某格中各字母的和所得多项式称为“特征多项式”.例如,第1格的“特征多项式”为4a+b.回答下列问题:
(1)第3格的“特征多项式”为 ,第4格的“特征多项式”为 ,第n格的“特征多项式”为 ;
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,求a,b的值.
| 序号 | 1 | 2 | 3 | … |
图形 | a a b a a | a a a b b a a b b a a a | a a a a b b b a a b b b a a b b b a a a a | … |
(1)第3格的“特征多项式”为
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,求a,b的值.
考点:规律型:图形的变化类
专题:
分析:(1)仔细观察每格的特征多项式的特点,找到规律,利用规律求得答案即可;
(2)根据题意列出二元一次方程组,求得a、b的值即可.
(2)根据题意列出二元一次方程组,求得a、b的值即可.
解答:解:(1)观察图形发现:
第1格的“特征多项式”为 4a+b,
第2格的“特征多项式”为 8a+4b,
第3格的“特征多项式”为 12a+9b,
第4格的“特征多项式”为16a+16b,
…
第n格的“特征多项式”为4na+n2b;
(2)∵第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,
∴
,
解得:a=-3;b=2,
∴a、b的值分别为-3和2.
第1格的“特征多项式”为 4a+b,
第2格的“特征多项式”为 8a+4b,
第3格的“特征多项式”为 12a+9b,
第4格的“特征多项式”为16a+16b,
…
第n格的“特征多项式”为4na+n2b;
(2)∵第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,
∴
|
解得:a=-3;b=2,
∴a、b的值分别为-3和2.
点评:本题考查了图形的变化类问题,解题的关键是仔细观察图形的变化,发现图形变化的规律,难度不大.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 如图,OA⊥OB、OC⊥OD,则∠l与∠2的大小关系是( )
如图,OA⊥OB、OC⊥OD,则∠l与∠2的大小关系是( )| A、∠1>∠2 |
| B、∠l=∠2 |
| C、∠l<∠2 |
| D、以上都不对 |
命题:
①对顶角相等;
②过一点有且只有一条直线与已知直线平行;
③相等的角是对顶角;
④同位角相等.
其中错误的有( )
①对顶角相等;
②过一点有且只有一条直线与已知直线平行;
③相等的角是对顶角;
④同位角相等.
其中错误的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△ABC中,AB=AC=5,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=
如图,在△ABC中,AB=AC=5,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=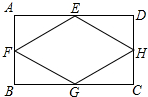 如图,E、F、G、H分别是矩形ABCD四边AB、BC、CD、AD的中点,
如图,E、F、G、H分别是矩形ABCD四边AB、BC、CD、AD的中点,