题目内容
已知二次函数y=-x2+4x-3.
(1)求二次函数与x轴有几个交点;
(2)求二次函数与坐标轴的交点.
(1)求二次函数与x轴有几个交点;
(2)求二次函数与坐标轴的交点.
考点:抛物线与x轴的交点
专题:
分析:(1)利用△与0的关系进行判断;
(2)设y=0,解方程,得到的解即为和x轴交点的横坐标,设x=0,得到的y值即为和y轴交点的纵坐标.
(2)设y=0,解方程,得到的解即为和x轴交点的横坐标,设x=0,得到的y值即为和y轴交点的纵坐标.
解答:解:(1)∵△=16-4×(-1)×(-3)=4>0,
∴函数图象与x轴有两个交点;
(2)设y=0,则0=-x2+4x-3,
解得:x=1或3,
所以二次函数与x轴的交点坐标为:(1,0)和(3,0),
设x=0,则y=-3,所以二次函数与y轴的交点坐标为:(0,-3)
综上可知二次函数与坐标轴的交点坐标为(1,0),(3,0),(0,-3).
∴函数图象与x轴有两个交点;
(2)设y=0,则0=-x2+4x-3,
解得:x=1或3,
所以二次函数与x轴的交点坐标为:(1,0)和(3,0),
设x=0,则y=-3,所以二次函数与y轴的交点坐标为:(0,-3)
综上可知二次函数与坐标轴的交点坐标为(1,0),(3,0),(0,-3).
点评:本题考查了抛物线和坐标轴的交点问题,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
相关题目
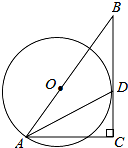 如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,延长BO交⊙O于点A,点D为⊙O上一点,过点A作直线BD的垂线,垂足为C,AD平分∠BAC.
如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,延长BO交⊙O于点A,点D为⊙O上一点,过点A作直线BD的垂线,垂足为C,AD平分∠BAC.(1)求证:BC是⊙O的切线;
(2)求AC的长.
比较368和451的大小关系是( )
| A、368>451 |
| B、368<451 |
| C、368=451 |
| D、无法判 |
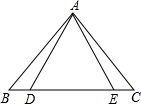 如图,△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于
如图,△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于 如图,一次函数y=-
如图,一次函数y=-