题目内容
7.在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:甲:79,81,82,85,83 乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是82,乙成绩的平均数是82;
(2)求甲、乙两名同学测试成绩的方差S甲2与S乙2.
(3)请你选择一个角度来判断选拔谁参加比赛更合适.
分析 (1)根据平均数的计算公式计算;
(2)利用方差公式进行计算即可;
(3)根据方差的性质解答.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{5}$(79+81+82+85+83)=82,
$\overline{{x}_{乙}}$=$\frac{1}{5}$(88+79+90+81+72)=82,
故答案为:82;82;
(2)S甲2=$\frac{1}{5}$[(79-82)2+(81-82)2+(82-82)2+(85-82)2+(83-82)2]=4,
S乙2=$\frac{1}{5}$[(88-82)2+(79-82)2+(90-82)2+(81-82)2+(72-82)2]=42,
(3)选拔甲参加比赛更合适,
因为甲的方差较小,成绩比较稳定.
点评 本题考查的是方差、平均数的计算,掌握算术平均数的计算公式、方差的计算公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
19.某中学八年级学生开展1分钟跳绳比赛活动,每班派5名学生参加,按团体总次数多少排列名次,在规定时间内每人跳100次以上(含100)为优秀,以下左表是成绩最好的(1)班和(2)班5名学生的比赛数据(单位:次):
经统计发现两班总次数相等.
(1)根据以上信息填写下表;
(2)若从中选派一个班级参加全市八年级跳绳比赛,综合以上的信息,你认为应选派哪一个班级参赛?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 方差 | |
| (1)班 | 89 | 100 | 96 | 118 | 97 | 94 |
| (2)班 | 100 | 95 | 110 | 91 | 104 | 44.4 |
| 优秀率 | 中位数 | |
| (1)班 | 40% | 97 |
| (2)班 | 60% | 100 |
(1)根据以上信息填写下表;
(2)若从中选派一个班级参加全市八年级跳绳比赛,综合以上的信息,你认为应选派哪一个班级参赛?简述你的理由.
16. 如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
 如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )
如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是( )| A. | 两点之间,直段最短 | B. | 两点确定一条直线 | ||
| C. | 两点之间,线段最短 | D. | 经过一点有无数条直线 |
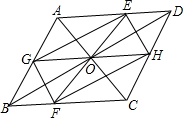 已知:如图,在?ABCD中,对角线AC、BD相交于点O,直线EF过点O,分别交AD、BC于点E、F,直线GH过点O,分别交AB,CD于点G、H.求证:四边形EGFH是平行四边形.
已知:如图,在?ABCD中,对角线AC、BD相交于点O,直线EF过点O,分别交AD、BC于点E、F,直线GH过点O,分别交AB,CD于点G、H.求证:四边形EGFH是平行四边形.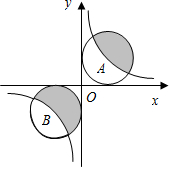 如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,则图中阴影部分的面积等于3π.
如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,则图中阴影部分的面积等于3π. 如图,C、D是线段AB上的两点,已知AC:CD:DB=1:2:3,M N分别是AC,BD的中点且AB=36cm,求线段MN的长.
如图,C、D是线段AB上的两点,已知AC:CD:DB=1:2:3,M N分别是AC,BD的中点且AB=36cm,求线段MN的长.