题目内容
15. 如图,已知一次函数${y_1}=\frac{2}{3}x+b$与反比例函数${y_2}=\frac{k}{x}$的图象交于A(3,4)、B(-6,n)两点.
如图,已知一次函数${y_1}=\frac{2}{3}x+b$与反比例函数${y_2}=\frac{k}{x}$的图象交于A(3,4)、B(-6,n)两点.(1)求反比例函数的解析式;
(2)观察图象,直接写出使一次函数值小于反比例函数值的x的取值范围;
(3)求△AOB的面积.
分析 (1)把点A坐标代入反比例函数求出k的值,也就求出了反比例函数解析式;
(2)根据图象和交点坐标即可求得;
(3)把点A的坐标代入${y_1}=\frac{2}{3}x+b$,求得一次函数解析式,求出直线与y轴的交点坐标,从而y轴把△AOB分成两个三角形,结合点A、B的横坐标分别求出两个三角形的面积,相加即可.
解答 解:(1)点A(3,4)在反比例函数${y_2}=\frac{k}{x}$的图象上,
∴k=3×4=12,
∴反比例函数的表达式为y2=$\frac{12}{x}$,
(2)一次函数值小于反比例函数值的x的取值范围是x<-6或0<x<3;
(3)把点A(3,4)代入一次函数${y_1}=\frac{2}{3}x+b$中,
得4=$\frac{2}{3}$×3+b,
解得b=2,
∴一次函数的表达式为y1=$\frac{2}{3}$x+2;
当x=0时,得y=2,
∴直线y1=$\frac{2}{3}$x+2与y轴的交点为C(0,2),
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×2×6+$\frac{1}{2}$×2×3=9.
点评 本题考查了反比例函数与一次函数图象的交点问题,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )
如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )
 如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )
如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )| A. | x1=3,x2=-2 | B. | x1=3,x2=-1 | C. | x1=1,x2=-1 | D. | x1=3,x2=-3 |
6.一条船沿南偏西50°方向航行到某地,然后沿原航线返回,返回时的航行方向是( )
| A. | 南偏东50° | B. | 南偏西50° | C. | 北偏东50° | D. | 北偏西50° |
3. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )| A. | 35° | B. | 40° | C. | 25° | D. | 30° |
10.下列各式中是一次函数的是( )
| A. | y=2(x-6)2 | B. | y=2(x-6) | C. | y=$\frac{2}{x-6}$ | D. | 2(x-6)=0 |
20.在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共20只,某学习小组作摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表示活动进行中的一组统计数据:
请估算口袋中白球约是( )只.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
| A. | 8 | B. | 9 | C. | 12 | D. | 13 |
7.下列说法,正确的是( )
| A. | 平方根是本身的数为0、1 | |
| B. | 0.125的立方根是$\frac{1}{2}$ | |
| C. | 无限小数是无理数,无理数也是无限小数 | |
| D. | 一个无理数和一个有理数之积为无理数 |
5.216表示( )
| A. | 2乘以16 | B. | 2个16相乘 | C. | 16个2相加 | D. | 16个2相乘 |
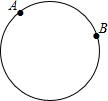 如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长).动点P从A点出发,以acm/s的速度,在轨道上逆时针方向运动,与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动,设运动时间为t(s),当t=5时,动点P、Q第一次相遇.
如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长).动点P从A点出发,以acm/s的速度,在轨道上逆时针方向运动,与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动,设运动时间为t(s),当t=5时,动点P、Q第一次相遇.