题目内容
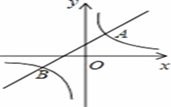
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(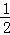 ,
,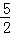 )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.

解:(1)∵B(4,m)在直线线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A( ,
, )、B(4,6)在抛物线y=ax2+bx﹣4上,
)、B(4,6)在抛物线y=ax2+bx﹣4上,
∴ ,
,
∵c=6,
∴a=2,b=﹣8,
∴y=2x2﹣8x+6.
(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),
∴PC=(n+2)﹣(2n2﹣8n+6),
=﹣2n2+9n﹣4,
=﹣2(n﹣ )2+
)2+ ,
,
∵PC>0,
∴当n= 时,线段PC最大且为
时,线段PC最大且为 .
.
(3)设直线AC的解析式为y=﹣x+b,
把A( ,
, )代入得:
)代入得: =﹣
=﹣ +b,解得:b=3,
+b,解得:b=3,
∴直线AC解析式:y=﹣x+3,
点C在抛物线上,设C(m,2m2﹣8m+6),代入y=﹣x+3得:2m2﹣8m+6=﹣m+3,
整理得:2m2﹣7m+3=0,
解得;m=3或m= ,
,
∴P(3,0)或P( ,
, ).
).

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列各式计算正确的是( )
|
| A. | a2+2a3=3a5 | B. | (a2)3=a5 | C. | a6÷a2=a3 | D. | a•a2=a3 |

 自变量x的取值范围是
自变量x的取值范围是  ,并写出它的非负整数解.
,并写出它的非负整数解. 从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )
从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )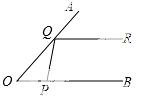
 :2x2﹣8=
:2x2﹣8=