题目内容
20.设A、B、C三点依次分别是抛物线y=x2-4x-5与y轴的交点以及与x轴的两个交点,则△ABC的面积是15.分析 分别求出抛物线与y轴的交点A和与x轴的交点B、C的坐标,得到线段BC的长,根据三角形面积公式求出面积即可.
解答 解:当x=0时,y=-5,点A的坐标(0,-5),
当y=0时,x2-4x-5=0,解得x1=-1,x2=5,
点B的坐标(-1,0),点C的坐标(5,0),则BC=6,
△ABC的面积为:$\frac{1}{2}$×6×5=15.
点评 本题考查的是抛物线与x轴的交点的求法,理解抛物线与x轴的交点的横坐标与一元二次方程的根的关系是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
15.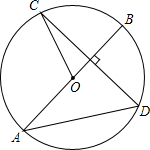 如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
 如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )
如图,线段AB是圆O的直径,弦CD⊥AB,如果∠BOC=70°,那么∠BAD等于( )| A. | 20° | B. | 30° | C. | 35° | D. | 70° |
5. 不等式组的解集在数轴上表示如图,则该不等式组是( )
不等式组的解集在数轴上表示如图,则该不等式组是( )
 不等式组的解集在数轴上表示如图,则该不等式组是( )
不等式组的解集在数轴上表示如图,则该不等式组是( )| A. | $\left\{\begin{array}{l}x≥-1\\ x≤2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<-1\\ x≥2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>-1\\ x<2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x>-1\\ x≤2\end{array}\right.$ |
10.将点A(-3,-2)向左平移5个单位,再向下平移4个单位得到点B,则点B的坐标为( )
| A. | (-8,2) | B. | (-8,-6) | C. | (2,-2) | D. | (2,2) |
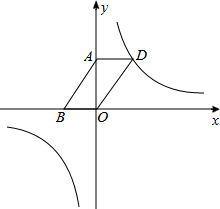 已知反比例函数$y=\frac{m-1}{x}$(m为常数)的图象在第一、三象限内.
已知反比例函数$y=\frac{m-1}{x}$(m为常数)的图象在第一、三象限内.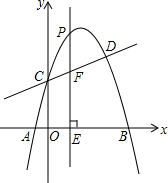 如图,抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C,D两点,其中点C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
如图,抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C,D两点,其中点C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.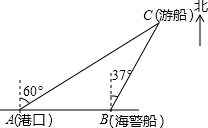 一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向.
一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向.