Question

9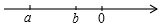．已知实数a、b在数轴上的对应点如图所示，化简$\sqrt{{a}^{2}}$+|a+b|+|$\sqrt{2}$-a|-$\sqrt{（b-\sqrt{2}）^{2}}$．

Answer 1

分析 根据数轴判断a、a+b、$\sqrt{2}$-a、b-$\sqrt{2}$与0的大小，然后根据绝对值的性质进行化简即可．

解答 解：由数轴可知：a＜b＜0，
∴a＜0，a+b＜0，
∵$\sqrt{2}$＞0，
∴$\sqrt{2}$-a＞0，b-$\sqrt{2}$＜0，
∴原式=|a|-（a+b）+$\sqrt{2}$-a-|b-$\sqrt{2}$|
=-a-a-b+$\sqrt{2}$-a+（b-$\sqrt{2}$）
=-3a-b+$\sqrt{2}$+b-$\sqrt{2}$
=-3a

点评 本题考查二次根式的性质，解题的关键是根据数轴判断a、a+b、$\sqrt{2}$-a、b-$\sqrt{2}$与0的大小，本题属于基础题型．