题目内容
9.点P(x,y)在反比例函数y=$\frac{1}{x}$的图象上,当x>2时,y的取值范围是0<y<$\frac{1}{2}$.分析 先根据反比例函数的性质判断出函数的增减性,再求出x=2时,y的值,即可得出结论.
解答 解:∵反比例函数y=$\frac{1}{x}$中,k>0,
∴此函数图象的两个分支位于第一、三象限,且在每一象限内,y随x的增大而减小,
∵当x=2时,y=$\frac{1}{2}$,
∴当x>2时,0<y<$\frac{1}{2}$.
故答案为:0<y<$\frac{1}{2}$.
点评 本题考查的是反比例函数的性质,熟知反比例函数的增减性是解答此题的关键.

练习册系列答案
相关题目
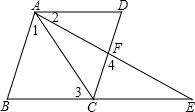 如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,问AD与BE平行吗?说说你的理由.
如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,问AD与BE平行吗?说说你的理由. 如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.
如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE. 如图是由6个大小相同的小正方体组成的几何体,它的主视图是( )
如图是由6个大小相同的小正方体组成的几何体,它的主视图是( )


