题目内容
2. 如图,圆柱形容器高14cm,底面圆的周长为24cm,在杯子内壁最底端B处有一滴蜂蜜,此时一只蚂蚁正好在杯子外壁且离杯子上沿2cm的A处,点A与点B处在杯子的相对位置.求蚂蚁从外壁A处到达内壁B处的最短距离.
如图,圆柱形容器高14cm,底面圆的周长为24cm,在杯子内壁最底端B处有一滴蜂蜜,此时一只蚂蚁正好在杯子外壁且离杯子上沿2cm的A处,点A与点B处在杯子的相对位置.求蚂蚁从外壁A处到达内壁B处的最短距离.
分析 将杯子侧面展开,作A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解答  解:如图:
解:如图:
将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=$\sqrt{A′{D}^{2}+B{D}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20(cm),
即蚂蚁从外壁A处到达内壁B处的最短距离为:20cm.
点评 本题考查了平面展开---最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若M和N都是关于x的二次三项式,则M+N一定是( )
| A. | 二次三项式 | B. | 一次多项式 | ||
| C. | 三项式 | D. | 次数不高于2的整式 |
12.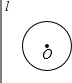 如图,⊙O的圆心O到直线m的距离为3cm,⊙O的半径为1cm,将直线m向右(垂直于m的方向)平移,使m与⊙O相切,则平移的距离为( )
如图,⊙O的圆心O到直线m的距离为3cm,⊙O的半径为1cm,将直线m向右(垂直于m的方向)平移,使m与⊙O相切,则平移的距离为( )
 如图,⊙O的圆心O到直线m的距离为3cm,⊙O的半径为1cm,将直线m向右(垂直于m的方向)平移,使m与⊙O相切,则平移的距离为( )
如图,⊙O的圆心O到直线m的距离为3cm,⊙O的半径为1cm,将直线m向右(垂直于m的方向)平移,使m与⊙O相切,则平移的距离为( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 2cm或4cm |
 如图,A,B,C,D四点在⊙O上,AD平分∠CDE,求证:$\widehat{AB}=\widehat{AC}$.
如图,A,B,C,D四点在⊙O上,AD平分∠CDE,求证:$\widehat{AB}=\widehat{AC}$. 如图,在△ABC中,∠A=90°,BD平分∠ABC,AD=5,则点到BC的距离为5.
如图,在△ABC中,∠A=90°,BD平分∠ABC,AD=5,则点到BC的距离为5.