题目内容
分解因式:
(1)x2-9;
(2)-3m2n-6mn-3n;
(3)4(m+n)2-9(m-n)2;
(4)(x+y)2-4(x+y-1).
(1)x2-9;
(2)-3m2n-6mn-3n;
(3)4(m+n)2-9(m-n)2;
(4)(x+y)2-4(x+y-1).
考点:提公因式法与公式法的综合运用
专题:
分析:(1)直接利用平方差公式分解因式即可;
(2)先提取公因式-3n,再对余下的多项式利用完全平方公式继续分解;
(3)利用平方差公式分解因式并整理即可得解;
(4)把(x+y)看作一个整体,展开后利用完全平方公式分解因式.
(2)先提取公因式-3n,再对余下的多项式利用完全平方公式继续分解;
(3)利用平方差公式分解因式并整理即可得解;
(4)把(x+y)看作一个整体,展开后利用完全平方公式分解因式.
解答:解:(1)x2-9=(x+3)(x-3);
(2)-3m2n-6mn-3n,
=-3n(m2+2m+1),
=-3n(m+1)2;
(3)4(m+n)2-9(m-n)2,
=[2(m+n)+3(m-n)][2(m+n)-3(m-n)],
=(2m+2n+3m-3n)(2m+2n-3m+3n),
=(5m-n)(5n-m);
(4)(x+y)2-4(x+y-1),
=(x+y)2-4(x+y)+4,
=(x+y-2)2.
(2)-3m2n-6mn-3n,
=-3n(m2+2m+1),
=-3n(m+1)2;
(3)4(m+n)2-9(m-n)2,
=[2(m+n)+3(m-n)][2(m+n)-3(m-n)],
=(2m+2n+3m-3n)(2m+2n-3m+3n),
=(5m-n)(5n-m);
(4)(x+y)2-4(x+y-1),
=(x+y)2-4(x+y)+4,
=(x+y-2)2.
点评:本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若∠A与∠B的两边分别平行,∠A=50°,则∠B=( )
| A、40° |
| B、50° |
| C、40°或140° |
| D、50°或130° |

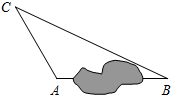 在一次课外实践活动中,同学们要知道校园内A、B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,并测得AC=60m,BC=140m,∠CAB=120°,请计算A、B两处之间的距离.
在一次课外实践活动中,同学们要知道校园内A、B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,并测得AC=60m,BC=140m,∠CAB=120°,请计算A、B两处之间的距离.