题目内容
3.如图是由同型号黑白两种颜色的正三角形瓷砖按一定规律铺设的图形.仔细观察图形可知:图①有1块黑色的瓷砖,可表示为1=$\frac{(1+1)×1}{2}$;图②有3块黑色的瓷砖,可表示为1+2=$\frac{(1+2)×2}{2}$;图③有6块黑色的瓷砖,可表示为1+2+3=$\frac{(1+3)×3}{2}$.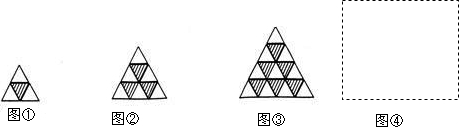
实践与探索:
(1)请在图④的虚线框内画出第4个图形,(只须画出草图)第4个图形有10块黑色的瓷砖;
(2)第n个图形有$\frac{1}{2}$n(n+1)块黑色的瓷砖(用含有n的代数式表示).
(3)求第21个图形有多少块黑色的瓷砖.
分析 (1)根据前面的3个图,则增加一行,就增加4块黑色的瓷砖;
(2)观察图形发现规律,进一步列出代数式,运用简便方法,即首尾相加进行计算;
(3)把n=21代入含有n的代数式计算得出答案即可.
解答 解:(1)如右图:
1+2+3+4=10;
(2)第n个图形有:1+2+3+…+n=$\frac{1}{2}$n(n+1)(n为正整数)
(3)当n=21时,$\frac{1}{2}$n(n+1)=$\frac{1}{2}$×21×(21+1)=231.
点评 此题考查图形的变化规律,找出图形与数字之间的运算规律,利用规律解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列关系式中,属于二次函数(x为自变量)的是( )
| A. | y=πx2 | B. | y=2x | C. | y=$\frac{1}{x}$ | D. | y=-x+1 |
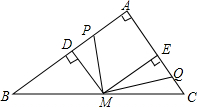 如图所示,P、Q分别是Rt△ABC两直角边AB、AC上两点,M为斜边BC的中点,且PM⊥QM,MD⊥AB于点D,ME⊥AC于点E.求证:
如图所示,P、Q分别是Rt△ABC两直角边AB、AC上两点,M为斜边BC的中点,且PM⊥QM,MD⊥AB于点D,ME⊥AC于点E.求证:
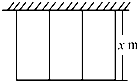 如图所示,一个农户用24m长的篱笆围成一排一面靠墙、大小相等且彼此相连的三个矩形鸡舍,要使三个鸡舍的总面积为36m2.如果设每个鸡舍的长为x m,根据题意列出的方程是(24-4x)•x=36.
如图所示,一个农户用24m长的篱笆围成一排一面靠墙、大小相等且彼此相连的三个矩形鸡舍,要使三个鸡舍的总面积为36m2.如果设每个鸡舍的长为x m,根据题意列出的方程是(24-4x)•x=36.