题目内容
5.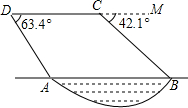 如图,某勘测飞机为了测量一湖泊两端A、B的距离,飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.
如图,某勘测飞机为了测量一湖泊两端A、B的距离,飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.
分析 过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,利用三角函数求出AE的长,在Rt△BDF中,利用三角函数求出BF的长,进而可得AB的长.
解答  解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
由题意可得∠ACD=63.4°,∠MDB=42.1°,CD=EF=125米,CE=DF=90米,
在Rt△AEC中,∠EAC=∠ACD=63.4°,
∵tan63.4°=$\frac{CE}{AE}$≈2.00,
∴AE=$\frac{CE}{tan63.4°}$≈$\frac{90}{2.00}$=45米,
在Rt△BDF中,∠FBD=∠MDB=42.1°,
∵tan42.1°=$\frac{DF}{BF}$≈0.90,
∴BF=$\frac{DF}{tan42.1°}$≈$\frac{90}{0.90}$=100米,
∴AB=EF-AE+BF=125-45+100=180米.
答:湖泊A、B两端的距离为180米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
| A. | 32,31 | B. | 31,32 | C. | 31,31 | D. | 32,35 |




 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.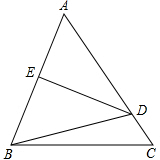 如图所示,△ABC为等腰三角形,AB=AC,AE=BE,AD=BD,∠DBC=15°,求∠ADE的度数.
如图所示,△ABC为等腰三角形,AB=AC,AE=BE,AD=BD,∠DBC=15°,求∠ADE的度数.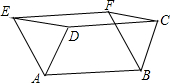 如图,已知?ABCD,以AD、BC为边,在它们的同侧作等边△ADE和等边△BCF,连接EF,求证:四边形ABFE和DCFE都是平行四边形.
如图,已知?ABCD,以AD、BC为边,在它们的同侧作等边△ADE和等边△BCF,连接EF,求证:四边形ABFE和DCFE都是平行四边形.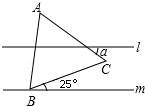 已知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为25°,则∠α的度数为35°.
已知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为25°,则∠α的度数为35°.