题目内容
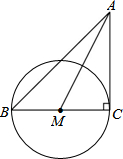如图，在Rt△ABC中，∠C=90°，以BC为直径作⊙M，连结AM，若sin∠CAM=| 3 |
| 5 |
考点：勾股定理,圆的认识,解直角三角形
专题：
分析：在直角三角形ACM中，利用锐角三角函数定义表示出sin∠CAM，由已知sin∠CAM的值，设CM=3x，得到AM=5x，根据勾股定理求出AC=4x，由M为BC的中点，得到BC=2CM，表示出BC，在直角三角形ABC中，利用锐角三角函数定义表示出tanB，将表示出的AC与BC代入即可求出值
解答：解：在Rt△ACM中，sin∠CAM=
=
，
设CM=3x，则AM=5x，
根据勾股定理得：AC=
=4x，
又M为BC的中点，
∴BC=2CM=6x，
在Rt△ABC中，tanB=
=
=
．
故答案是：
．
| CM |
| AM |
| 3 |
| 5 |
设CM=3x，则AM=5x，
根据勾股定理得：AC=
| AM2-CM2 |
又M为BC的中点，
∴BC=2CM=6x，
在Rt△ABC中，tanB=
| AC |
| BC |
| 4x |
| 6x |
| 2 |
| 3 |
故答案是：
| 2 |
| 3 |
点评：此题考查了解直角三角形，锐角三角函数定义，以及勾股定理，熟练掌握锐角三角函数定义是解本题的关键．
练习册系列答案
寒假学与练系列答案
相关题目
如图，直线y=-x+b（b＞0）与双曲线y=
将一块直尺与一块三角板如图2放置，若∠1=45°，则∠2的度数为（ ）| A、145° | B、135° |
| C、120° | D、115° |
-5的相反数是（ ）
A、
| ||
B、-
| ||
| C、-5 | ||
| D、5 |