题目内容
2.已知抛物线y=2x2-8x+k+8和直线y=mx+1相交于点P(3,4m),求这两个函数的解析式及另一交点坐标.分析 先把P(3,4m)代入y2=mx+1求出m,从而得到一次函数解析式,且确定P点坐标,然后把P点坐标代入y1=2x2-8x+k+8求出k的值,于是可确定抛物线解析式;联立方程,解方程可确定抛物线与直线的另一个交点坐标.
解答 解:把P(3,4m)代入y2=mx+1得3m+1=4m,解得m=1,
所以一次函数解析式为y=x+1,
把P(3,4)代入y1=2x2-8x+k+8得2×9-8×3+k+8=4,解得k=2,
所以抛物线解析式为y1=2x2-8x+10;
解$\left\{\begin{array}{l}{y=2{x}^{2}-8x+10}\\{y=x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{5}{2}}\end{array}\right.$
所以,抛物线与直线的另一个交点坐标为($\frac{3}{2}$,$\frac{5}{2}$).
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11.一元二次方程x2-16=0的根是( )
| A. | x=2 | B. | x=4 | C. | x1=2,x2=-2 | D. | x1=4,x2=-4 |
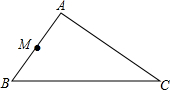 如图,已知△ABC中,AB=4,AC=6,BC=9,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.
如图,已知△ABC中,AB=4,AC=6,BC=9,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.