��Ŀ����
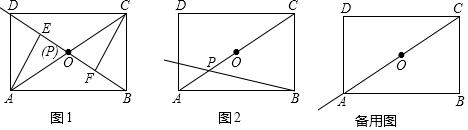
9�� ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬Rt��ABO�ı�AB��ֱ��x�ᣬ����Ϊ��B������������y1=$\frac{{k}_{1}}{x}$��x��0����ͼ��AO���е�C������AB�ཻ�ڵ�D��OB=4��AB=3��
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬Rt��ABO�ı�AB��ֱ��x�ᣬ����Ϊ��B������������y1=$\frac{{k}_{1}}{x}$��x��0����ͼ��AO���е�C������AB�ཻ�ڵ�D��OB=4��AB=3����1����������y1=$\frac{{k}_{1}}{x}$��x��0���Ľ���ʽ��
��2���辭��C��D�����һ�κ�������ʽΪy2=k2x+b����������ʽ��������ͼ��ֱ��д���ڵ�һ�����ڣ���y2��y1ʱ��x��ȡֵ��Χ��
���� ��1������OB��AB�ij��ȿɵó���A�����꣬�ɵ�CΪ�߶�OA���е㼴�ɵó���C�����꣬���ݵ�C���������÷���������ͼ���ϵ�������������������������������ʽ��
��2���ɵ�D�ĺ������Ϸ���������ͼ���ϵ�������������������D�����꣬���ݵ�C��D���������ô���ϵ�����������һ�κ�������ʽ���ٸ���������ͼ�������λ�ù�ϵ���ɵó�����ʽ�Ľ⼯��
��� �⣺��1����OB=4��AB=3����A�ڵ�һ���ޣ�
���A��������4��3����
�ߵ�CΪ�߶�OA���е㣬
���C��������2��$\frac{3}{2}$����
�ߵ�C�ڷ���������y1=$\frac{{k}_{1}}{x}$��x��0����ͼ���ϣ�
��k1=2��$\frac{3}{2}$=3��
�෴���������Ľ���ʽΪy=$\frac{3}{x}$��x��0����
��2����x=4ʱ��y=$\frac{3}{4}$��
���D��������4��$\frac{3}{4}$����
��C��2��$\frac{3}{2}$����B��4��$\frac{3}{4}$������y2=k2x+b��
$\left\{\begin{array}{l}{2{k}_{2}+b=\frac{3}{2}}\\{4{k}_{2}+b=\frac{3}{4}}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{k}_{2}=-\frac{3}{8}}\\{b=\frac{9}{4}}\end{array}\right.$��
��һ�κ�������ʽΪy2=-$\frac{3}{8}$x+$\frac{9}{4}$��
�۲캯��ͼ���֪����2��x��4ʱ��һ�κ���ͼ���ڷ���������ͼ����Ϸ���
�൱y2��y1ʱ��x��ȡֵ��ΧΪ2��x��4��
���� ���⿼���˷�����������һ�κ����Ľ������⡢����������ͼ���ϵ�����������Լ�����ϵ������������ʽ�����ݵ���������ô���ϵ���������������ʽ�ǽ���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��x3��2=x5 | B�� | ��2x��2=2x2 | C�� | ��x+1��3•x2=x5 | D�� | x3•x2=x5 |








 ��ͼ������OA�ķ����DZ�ƫ��20�㣬����OB�ķ����DZ�ƫ��40�㣬OD��OB�ķ����ӳ��ߣ���OC�ǡ�AOD��ƽ���ߣ����BOC=120�㣬����OC�ķ����DZ�ƫ��80�㣮
��ͼ������OA�ķ����DZ�ƫ��20�㣬����OB�ķ����DZ�ƫ��40�㣬OD��OB�ķ����ӳ��ߣ���OC�ǡ�AOD��ƽ���ߣ����BOC=120�㣬����OC�ķ����DZ�ƫ��80�㣮 ��֪������G1��y=a��x-h��2+2�ĶԳ���Ϊx=-1���Ҿ���ԭ�㣮
��֪������G1��y=a��x-h��2+2�ĶԳ���Ϊx=-1���Ҿ���ԭ�㣮