题目内容
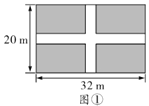
【题目】为了美化校园,某校要在如图①所示的长![]() ,宽
,宽![]() 的矩形地面上修等宽的人行道,余下的部分进行绿化.
的矩形地面上修等宽的人行道,余下的部分进行绿化.
(1)设人行道宽为![]() ,用含
,用含![]() 的式子表示绿化面积;
的式子表示绿化面积;
(2)如果要使绿化面积为![]() ,求出此时人行道的宽;
,求出此时人行道的宽;
(3)已知某园林公司修筑人行道、绿化的造价![]() (元)、
(元)、![]() (元)与修建面积
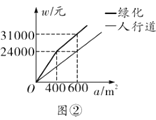
(元)与修建面积![]() 之间的函数关系如图②所示,如果该校决定由该公司承建此项目,并要求修建的人行道的宽度不少于
之间的函数关系如图②所示,如果该校决定由该公司承建此项目,并要求修建的人行道的宽度不少于![]() 且不超过
且不超过![]() ,那么人行道宽为多少时,修建的人行道和绿化的总造价最低,最低总造价为多少元?
,那么人行道宽为多少时,修建的人行道和绿化的总造价最低,最低总造价为多少元?
【答案】(1)![]() ;(2)人行道的宽为
;(2)人行道的宽为![]() ;(3)当人行道宽为
;(3)当人行道宽为![]() 时,修建的人行道和绿化的总造价最低,最低为31360元.
时,修建的人行道和绿化的总造价最低,最低为31360元.
【解析】
(1)根据图1列式即可;
(2)令![]() ,然后求得x的值即可;
,然后求得x的值即可;
(3) 设修建的人行道和绿化的总造价为![]() 元.则由题意得
元.则由题意得![]() ,然后再求得
,然后再求得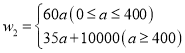 ,进而求得b的最大值和最小值;最后分
,进而求得b的最大值和最小值;最后分![]() 和
和![]() 两种情况解答即可.
两种情况解答即可.
解:(1)设人行道宽为![]() ,则绿化的面积为
,则绿化的面积为![]() ;
;
(2)根据题意,得![]() ,
,
解得:![]() ,
,![]() (舍去),故人行道的宽为
(舍去),故人行道的宽为![]() ;
;
(3)设修建的人行道和绿化的总造价为![]() 元.由题图可知:
元.由题图可知:![]() ,
,
当![]() 时,设
时,设![]() ,将(400,24000)和(600,31000)代入
,将(400,24000)和(600,31000)代入![]() 得
得![]() ,
,
解得![]() ,
,
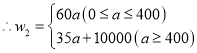 ,
,
设绿化的面积为![]() ,则人行道的面积为
,则人行道的面积为![]() ,
,
![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,因此,
,因此,![]() ,
,
于是分两种情况:
①当![]() 时,
时,
![]() ,
,
![]() ,
,![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 当
当![]() 时,
时,![]() 最小,
最小,![]() .此时
.此时![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
因此,当![]() ,人行道宽为
,人行道宽为![]() 时,修建的人行道和绿化的总造价最低,最低为31360元;
时,修建的人行道和绿化的总造价最低,最低为31360元;
②当![]() 时,
时,
![]() ,
,
![]() ,
,![]() 随
随![]() 的增大而减小,
的增大而减小,
![]() 当
当![]() 时,
时,![]() 最小,
最小,![]() .
.
此时![]() ,解得:
,解得:![]() 或
或![]() (舍去),
(舍去),
因此,当![]() ,人行道宽为
,人行道宽为![]() 时,修建的人行道和绿化的总造价最低,最低为33135元,
时,修建的人行道和绿化的总造价最低,最低为33135元,
![]() ,
,
![]() 当人行道宽为
当人行道宽为![]() 时,修建的人行道和绿化的总造价最低,最低为31360元.
时,修建的人行道和绿化的总造价最低,最低为31360元.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目