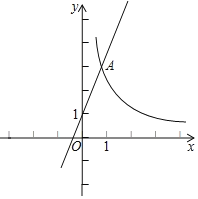ЬтФПФкШн
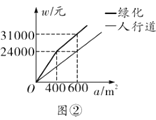
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊзјБъдЕуЃЌХзЮяЯп
ЮЊзјБъдЕуЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
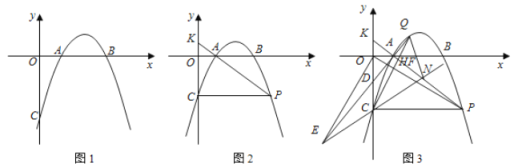
ЃЈ1ЃЉШчЭМ1ЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() ЮЊХзЮяЯпЩЯвЛЕуЃЌСЌНг
ЮЊХзЮяЯпЩЯвЛЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌШєЕу
ЃЌШєЕу![]() ЕФКсзјБъЮЊ4ЃЌЧѓ
ЕФКсзјБъЮЊ4ЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
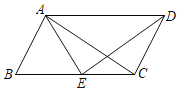
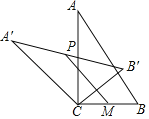
ЃЈ3ЃЉШчЭМ3ЃЌЕу![]() ЮЊЖдГЦжсгвВрЕкЫФЯѓЯоХзЮяЯпЩЯвЛЕуЃЌСЌНг
ЮЊЖдГЦжсгвВрЕкЫФЯѓЯоХзЮяЯпЩЯвЛЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЎСЌНг
ЃЎСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() бгГЄЯпгкЕу
бгГЄЯпгкЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌбгГЄ
ЪБЃЌбгГЄ![]() НЛХзЮяЯпгкЕу
НЛХзЮяЯпгкЕу![]() ЃЌЕу
ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌНЛЯпЖЮ
ЃЌНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌНЋЩфЯп
ЃЌНЋЩфЯп![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ45ЁуЃЌЕУЕНЩфЯп
ФцЪБеыа§зЊ45ЁуЃЌЕУЕНЩфЯп![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпНтЮіЪНЮЊ![]() ЃЛЃЈ2ЃЉ8ЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉ8ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЯШНЋ![]() ЕФКсзјБъДњШыХзЮяЯпЗНГЬЧѓГіPЕуЕФзјБъЃЌдйЙ§Еу
ЕФКсзјБъДњШыХзЮяЯпЗНГЬЧѓГіPЕуЕФзјБъЃЌдйЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌгЩЯжгаЬѕМўЭЦГіCKЕФжЕЃЌМДПЩЧѓГіД№АИЃЛ
ЃЌгЩЯжгаЬѕМўЭЦГіCKЕФжЕЃЌМДПЩЧѓГіД№АИЃЛ
ЃЈ3ЃЉЪзЯШЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЩш
ЃЌЩш![]() ЃЌЧѓГіtжЕЃЌдйЙ§Еу
ЃЌЧѓГіtжЕЃЌдйЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШЗЖЈQЕузјБъЮЊЃЈ2ЃЌ1ЃЉЃЌAT=BT=1ЃЌЭЦГі
ЃЌШЗЖЈQЕузјБъЮЊЃЈ2ЃЌ1ЃЉЃЌAT=BT=1ЃЌЭЦГі![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЃЌВЂНиШЁ
жсЃЌВЂНиШЁ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЭЦГі
ЃЌЭЦГі![]() ЃЌЭЦГі
ЃЌЭЦГі![]() ЃЌДгЖјжЄУї
ЃЌДгЖјжЄУї![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЭЦГі
ЃЌЭЦГі![]() ЃЌЭЦГі
ЃЌЭЦГі![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЃЌЕу
ЃЌЕу![]() ЃЌЫљЧѓНтЮіЪНЮЊ
ЃЌЫљЧѓНтЮіЪНЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() бгГЄЯпЕФДЙЯпЃЌНЛгкЕу
бгГЄЯпЕФДЙЯпЃЌНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЃЌгЩ
ЃЌгЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌЕу
ЃЌЕу![]() гыЕу
гыЕу![]() жиКЯЃЌЩшЕу
жиКЯЃЌЩшЕу![]() ЃЌ
ЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌМДПЩЕУГі
ЃЌМДПЩЕУГі![]() ЃЎ
ЃЎ
ЃЈ1ЃЉНЋAЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉДњШыХзЮяЯпНтЮіЪН
ЕУ![]() ЃЌ
ЃЌ
НтЕУ![]()
ЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпЕу![]() ЕФКсзјБъЮЊ4ЃЌДњШыХзЮяЯпЗНГЬПЩЕУЕу
ЕФКсзјБъЮЊ4ЃЌДњШыХзЮяЯпЗНГЬПЩЕУЕу![]() ЕФзјБъЮЊЃЈ4ЃЌ-3ЃЉЃЌгжCЃЈ0ЃЌ-3ЃЉЃЌ
ЕФзјБъЮЊЃЈ4ЃЌ-3ЃЉЃЌгжCЃЈ0ЃЌ-3ЃЉЃЌ
![]() жсЃЌ
жсЃЌ
![]() ЃЌ
ЃЌ
ШчЭМ1ЫљЪОЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌ
ЃЌ
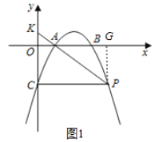
![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ2ЫљЪОЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ
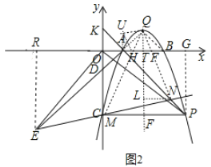
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Й§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ
ЩшЕу![]() ЃЌгЩ
ЃЌгЩ![]() ПЩЕУ
ПЩЕУ![]() ЃЌ
ЃЌ
НтЕУ![]() Лђ2ЃЌ
Лђ2ЃЌ
ЁрЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Й§Еу![]() зї
зї![]() жсЃЌВЂНиШЁ
жсЃЌВЂНиШЁ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЩшжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ
дђжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Й§Еу![]() зї
зї![]() бгГЄЯпЕФДЙЯпЃЌНЛгкЕу
бгГЄЯпЕФДЙЯпЃЌНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЃЌ
ЃЌ
гЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌЕу
ЃЌЕу![]() гыЕу
гыЕу![]() жиКЯЃЌЩшЕу
жиКЯЃЌЩшЕу![]() ЃЌ
ЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ

 ЧсЫЩПЮЬУЕЅдЊВтЪдABОэЯЕСаД№АИ
ЧсЫЩПЮЬУЕЅдЊВтЪдABОэЯЕСаД№АИ аЁЬтПёзіЯЕСаД№АИ
аЁЬтПёзіЯЕСаД№АИ