题目内容
 已知二次函数y=-
已知二次函数y=-| 1 |
| 2 |
| 3 |
| 2 |
(1)求图象的对称轴,顶点坐标;
(2)求图象与x轴的交点坐标,与y轴的交点坐标;
(3)根据(1)和(2)的答案画出草图,观察图象,当x为何值时,y随x的增大而增大?当x为何值时y≥0?
考点:二次函数的性质,二次函数的图象
专题:
分析:(1)利用配方法确定二次函数的顶点坐标及对称轴即可;
(2)抛物线的解析式中,令x=0,可求得与y轴交点坐标;令y=0,可求得与x轴的交点坐标;
(3)根据确定的对称轴及与坐标轴的交点坐标可作出二次函数的图象;根据对称轴及开口方向利用图象直接叙述其增减性;当图象在x轴及其上方时y≥0,据此写出x的取值范围.
(2)抛物线的解析式中,令x=0,可求得与y轴交点坐标;令y=0,可求得与x轴的交点坐标;
(3)根据确定的对称轴及与坐标轴的交点坐标可作出二次函数的图象;根据对称轴及开口方向利用图象直接叙述其增减性;当图象在x轴及其上方时y≥0,据此写出x的取值范围.
解答:解:(1)∵y=-
x2-x-
=-
(x2+2x+1+2)=-
(x+1)2-1,
∴对称轴为x=-1,顶点坐标为(-1,-1);
(2)令x=0,则y=-
,
所以函数y=-
x2-x-
与y轴的交点坐标为(0,-
);
令y=0,则-
x2-x-
=0,即x2+2x+3=0,
∵△=b2-4ac<0,
∴与x轴无交点;
(3)图象为:
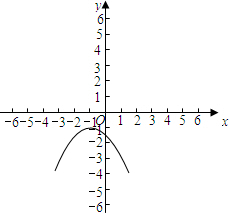
当x<-1时,y随x的增大而增大;x取任何值,都不能使得y≥0.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴对称轴为x=-1,顶点坐标为(-1,-1);
(2)令x=0,则y=-
| 3 |
| 2 |
所以函数y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
令y=0,则-
| 1 |
| 2 |
| 3 |
| 2 |
∵△=b2-4ac<0,
∴与x轴无交点;
(3)图象为:

当x<-1时,y随x的增大而增大;x取任何值,都不能使得y≥0.
点评:此题考查了二次函数的性质与图象,考查了通过配方法求顶点式,求顶点坐标,对称轴;还考查了根据对称轴了解二次函数的增减性及观察图象回答问题的能力.

练习册系列答案
相关题目
下列结论中,错误的是( )
| A、如果a+b=0,那么a与b互为相反数 |
| B、如果ab=1,那么a与b互为倒数 |
| C、如果ab>0,那么a与b同号 |
| D、如果|x|=3,那么x=3 |
 如图,△ABC中AC⊥BC,AC=8cm,BC=4cm,AP⊥AC于A,现有两点D、E分别在AC和AP上运动,运动过程中总有DE=AB,问D在AC上运动到什么位置时,能使△ADE和△ABC全等?
如图,△ABC中AC⊥BC,AC=8cm,BC=4cm,AP⊥AC于A,现有两点D、E分别在AC和AP上运动,运动过程中总有DE=AB,问D在AC上运动到什么位置时,能使△ADE和△ABC全等?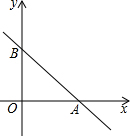 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.