题目内容
16.已知x1=3,xn=1$-\frac{1}{{x}_{n-1}}$(n=2,3,4…).(1)求x2,x3,x4,x5;
(2)求x2000.
分析 (1)根据x1=3,xn=1-$\frac{1}{{x}_{n-1}}$,确定出所求即可;
(2)归纳总结得到一般性规律,即可确定出x2000.
解答 解:(1)把x1=3,代入得:x2=1-$\frac{1}{{x}_{1}}$=$\frac{2}{3}$,x3=1-$\frac{1}{{x}_{2}}$=1-$\frac{3}{2}$=-$\frac{1}{2}$,x4=1-$\frac{1}{{x}_{3}}$=3,x5=1-$\frac{1}{{x}_{4}}$=$\frac{2}{3}$;
(2)根据(1)得到其值以3,$\frac{2}{3}$,-$\frac{1}{2}$循环,
∵2000÷3=666…2,
∴x2000=$\frac{2}{3}$.
点评 此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.有一批袋装食品,标准质量为每袋50g,现抽取10袋样品进行检测.结果如下(单位:g):48,51,52,49,53,52,48,49,50,52.
(1)请你用正、负数表示每袋食品与标准质量的差值,并填在表中:
(2)请你计算表中的差值的和;
(3)请你计算这10袋样品食品的总质量.
(1)请你用正、负数表示每袋食品与标准质量的差值,并填在表中:
| 袋号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 与标准质量的差值 |
(3)请你计算这10袋样品食品的总质量.
8.已知三个有理数a,b,c的积是正数,它们的和是负数,当x=$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$时,求代数式:-3x19-2008x-2013的值.
6. 如图,抛物线顶点坐标是P(1,2),函数y随自变量x的增大而减小的x的取值范围是( )
如图,抛物线顶点坐标是P(1,2),函数y随自变量x的增大而减小的x的取值范围是( )
 如图,抛物线顶点坐标是P(1,2),函数y随自变量x的增大而减小的x的取值范围是( )
如图,抛物线顶点坐标是P(1,2),函数y随自变量x的增大而减小的x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x>1 | D. | x<1 |
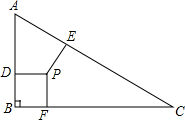 某小区有一块直角三角形空地,如图所示,∠B=90°,AB=7m,BC=24m,AC=25m,物业管理员准备把这块空地进行绿化,在三角形中找一点P,各每边修一条垂直小经,小径到各边距离相等,问三条小径,共有多长?
某小区有一块直角三角形空地,如图所示,∠B=90°,AB=7m,BC=24m,AC=25m,物业管理员准备把这块空地进行绿化,在三角形中找一点P,各每边修一条垂直小经,小径到各边距离相等,问三条小径,共有多长?