题目内容
4.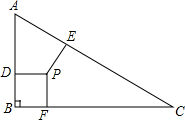 某小区有一块直角三角形空地,如图所示,∠B=90°,AB=7m,BC=24m,AC=25m,物业管理员准备把这块空地进行绿化,在三角形中找一点P,各每边修一条垂直小经,小径到各边距离相等,问三条小径,共有多长?
某小区有一块直角三角形空地,如图所示,∠B=90°,AB=7m,BC=24m,AC=25m,物业管理员准备把这块空地进行绿化,在三角形中找一点P,各每边修一条垂直小经,小径到各边距离相等,问三条小径,共有多长?
分析 连接PA、PB、PC,根据三角形面积公式计算即可.
解答 解: 连接PA、PB、PC,
连接PA、PB、PC,
∵小径到各边距离相等,
∴PF=PD=PE,
$\frac{1}{2}$×BC×PF+$\frac{1}{2}$×AB×PD+$\frac{1}{2}$×AC×PE=$\frac{1}{2}$×BC×AB,
∴PF=PD=PE=3,
则PF+PD+PE=9,
∴三条小径共有9米.
点评 本题考查的是角平分线的性质和三角形的面积计算,掌握三角形面积公式是解题的关键.

练习册系列答案
相关题目
14.若单项式2xnym-n与单项式3xny2n的和是5xny2n,则m,n的关系是( )
| A. | m=n | B. | m=2n | C. | m=3n | D. | m=4n |
19.填写下表.并问答有关问题:
请认真观察你所填写的数字.看看有没有什么规律?然后猜想,如果x1与x2互为相反数,那么s1与s2的关系为相等.
| x | x1 | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … | x2 |
| x2-4 | s1 | … | … | s2 |

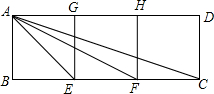 如图,矩形ABCD是由三个完全相同的正方形ABEG、GEFH、HFCD组成的,证明:△FEA∽△AEC.
如图,矩形ABCD是由三个完全相同的正方形ABEG、GEFH、HFCD组成的,证明:△FEA∽△AEC.