题目内容
规定一种新运算，a?b=a+b，a⊕b=a-b，其中a、b为有理数，则化简式子（a2b?5ab）-2（a2b⊕3ab），并求出当a=3，b=-1时，式子的值是多少？
考点：整式的加减—化简求值
专题：新定义
分析：原式利用题中的新定义化简，去括号合并得到最简结果，把a与b的值代入计算即可求出值．
解答：解：利用题中的新定义得：原式=a2b+5ab-2（a2b-3ab）=a2b+5ab-2a2b+6ab=-a2b+11ab，
当a=3，b=-1时，原式=9-33=-24．
当a=3，b=-1时，原式=9-33=-24．
点评：此题考查了整式的加减-化简求值，弄清题中的新定义是解本题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
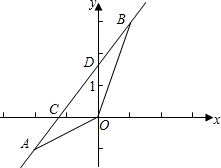如图，已知A（-2，-1），B（1，3）两点在一次函数y=
如图，BD为⊙O的直径，点A是弧BC的中点，AD交BC于E点，DF是⊙O的切线与BC的延长线交于点F，AE=2，ED=4，下列结论：①△ABE∽△ABD；②AB=2