题目内容
(1)
-
(2)
÷
(3)
-
(4)(-1)2013+(3-π)0+(
)-1.
| x2 |
| x-y |
| y2 |
| x-y |
(2)
| m |
| m2-1 |
| m2+m |
| m2 |
(3)
| a |
| a-1 |
| 2a |
| a2-1 |
(4)(-1)2013+(3-π)0+(
| 1 |
| 2 |
考点:分式的混合运算,零指数幂,负整数指数幂
专题:
分析:(1)根据同分母的分式进行加减即可;
(2)根据分式的除法法则进行计算即可;
(3)先通分,再根据同分母的分式进行加减即可;
(4)根据零指数幂、负整数指数幂进行计算即可.
(2)根据分式的除法法则进行计算即可;
(3)先通分,再根据同分母的分式进行加减即可;
(4)根据零指数幂、负整数指数幂进行计算即可.
解答:解:(1)原式=
=
=x+y;
(2)原式=
•
=
;
(3)原式=
-
=
-
=
=
=
;
(4)原式=-1+1+2
=2.
| x2-y2 |
| x-y |
=
| (x+y)(x-y) |
| x-y |
(2)原式=
| m |
| (m+1)(m-1) |
| m2 |
| m(m+1) |
| m2 |
| m-1 |
(3)原式=
| a |
| a-1 |
| 2a |
| (a+1)(a-1) |
=
| a(a+1) |
| (a+1)(a-1) |
| 2a |
| (a+1)(a-1) |
=
| a2+a-2a |
| (a+1)(a-1) |
=
| a(a-1) |
| (a+1)(a-1) |
=
| a |
| a+1 |
(4)原式=-1+1+2
=2.
点评:本题考查了分式的混合运算以及零指数幂和负整数指数幂进行计算,通分、因式分解和约分是解答的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
如图是深圳地铁交通图的一部分,小明要坐地铁从世界之窗站到科学馆站,他选择了坐地铁1号线直达,用数学知识解释其选择的原因,可以为( )
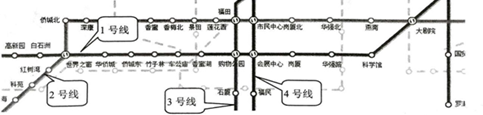

| A、两点之间,线段最短 |
| B、两点确定一条直线 |
| C、两点之间线段的长度,叫做这两点之间的距离 |
| D、过一点有无数条直线 |
 如图,AB是⊙O的直径,D为
如图,AB是⊙O的直径,D为 |
| AC |
| A、80° | B、100° |
| C、110° | D、140° |
-3的倒数是( )
A、
| ||
B、-
| ||
| C、3 | ||
| D、-3 |
若-2xmyn+2与3x2y是同类项,则nm的值为( )
| A、9 | B、1 | C、-1 | D、0 |
 如图,图中阴影部分是一个正方形,这个正方形的对角线长为
如图,图中阴影部分是一个正方形,这个正方形的对角线长为