题目内容
18．
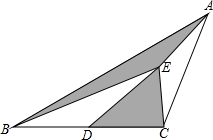如图所示，AD是△ABC的中线，点E是AD的中点，连接BE、CD，若△ABC的面积为7，则阴影部分的面积为$\frac{7}{2}$．
分析 由AD是△ABC的中线，可得S△ABD=S△ACD=$\frac{1}{2}$S△ABC，同理可得S△ABE=S△ADE=$\frac{1}{2}$S△ABD，S△CDE=S△CAE=$\frac{1}{2}$S△ACD，得出S△ABE=$\frac{1}{4}$S△ABC，S△CDE=$\frac{1}{4}$S△ABC，即可求得S△ABE+S△CDE=$\frac{1}{2}$S△ABC=$\frac{7}{2}$．
解答 解：∵AD是△ABC的中线，
∴S△ABD=S△ACD=$\frac{1}{2}$S△ABC：
∵点E是AD的中点，
∴S△ABE=S△ADE=$\frac{1}{2}$S△ABD，S△CDE=S△CAE=$\frac{1}{2}$S△ACD，
∵S△ABE=$\frac{1}{4}$S△ABC，S△CDE=$\frac{1}{4}$S△ABC，
∴S△ABE+S△CDE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×7=$\frac{7}{2}$；
∴阴影部分的面积为 $\frac{7}{2}$，
故答案为$\frac{7}{2}$．
点评 本题主要考查了三角形面积及三角形面积的等积变换，三角形的中线将三角形分成面积相等的两部分．
练习册系列答案
相关题目
如图所示，已知△ADE≌△BCF，AD=6cm，CD=5cm，求BD的长．
如图，△ABD≌△ECD，∠ECA=70°，∠A=30°，AB=6cm．求：∠E、∠D、∠DBA的度数及CE的长．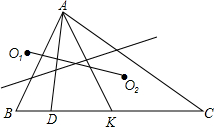
设D是△ABC的边BC上一点，但不是中点，设O1和O2分别是△ABD和△ADC的外心，求证：△ABC的中线AK的垂直平分线过线段O1O2中点．
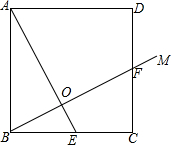已知：正方形ABCD，E是BC的中点，连接AE，过点B作射线BM交正方形的一边于点F，交AE于点O．