题目内容
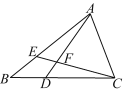
【题目】如图，在△ABC中，点E在AB上，点D在BC上，BD＝BE，∠BAD＝∠BCE，AD与CE相交于点F，试判断△AFC的形状，并说明理由．
【答案】△AFC是等腰三角形．理由见解析．
【解析】
试题根据条件证明△BAD≌△BCE从而得出BA=BC，∠BAD=∠BCE，然后结合条件证明∠FAC=∠FCA即可．
试题解析：△AFC是等腰三角形．理由如下：
在△BAD与△BCE中，
∵∠B=∠B（公共角），∠BAD=∠BCE，BD=BE，
∴△BAD≌△BCE（AAS），
∴BA=BC，∠BAD=∠BCE，
∴∠BAC=∠BCA，
∴∠BAC﹣∠BAD=∠BCA﹣∠BCE，即∠FAC=∠FCA．
∴AF=CF，
∴△AFC是等腰三角形．
练习册系列答案
相关题目
【题目】体育文化用品商店购进篮球和排球共20个，进价和售价如下表，全部销售完后共获利润260元．
篮球 | 排球 | |
进价（元/个） | 80 | 50 |
售价（元/个） | 95 | 60 |
求：（1）购进篮球和排球各多少个？
（2）销售6个排球的利润与销售几个篮球的利润相等？
