题目内容
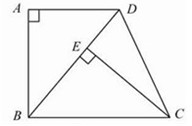
如图，在梯形ABCD中，AB∥CD，∠A=60°，∠B=30°，若AD=CD=6，则AB的长等于
| A．9 | B．12 | C． | D．18 |
D
分别过D点，C点作DE⊥AB，CF⊥AB，垂足分别为E，F．
∵∠A=60°，DE⊥AB，∴∠ADE=30°，∴AE=
AD=×6=3．
∴DE=
∵AB∥CD，∴CDEF是矩形，∴CD=EF，DE=CF=
，
∵∠B=30°，CF⊥AB，∴BC=
，FB=
=9，
∴AB=AE+EF+FB=3+6+9=18．故选D.
∵∠A=60°，DE⊥AB，∴∠ADE=30°，∴AE=
AD=×6=3．∴DE=
∵AB∥CD，∴CDEF是矩形，∴CD=EF，DE=CF=，∵∠B=30°，CF⊥AB，∴BC=
，FB==9，∴AB=AE+EF+FB=3+6+9=18．故选D.
练习册系列答案
相关题目
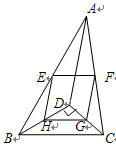
，折叠后，点C落在AD边上的C1处，并且点B落在EC1边上的B1处．则BC的长为（ ）
