题目内容
如图，在平面直角坐标系中，矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，OC=2，则点B的坐标是
（2，2
）。
）。过点B作DE⊥OE于E，
∵矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，
∴∠CAO=30°。
又∵OC=2，∴AC=4。∴OB=AC=4。
又∵∠OBC=∠CAO=30°，DE⊥OE，∠CBA=90°，∴∠OBE=30°。
∴OE=2，BE="OB·cos∠OBE" =2。
∴点B的坐标是（2，2）。
∵矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，
∴∠CAO=30°。
又∵OC=2，∴AC=4。∴OB=AC=4。
又∵∠OBC=∠CAO=30°，DE⊥OE，∠CBA=90°，∴∠OBE=30°。
∴OE=2，BE="OB·cos∠OBE" =2
。∴点B的坐标是（2，2
）。
练习册系列答案
相关题目
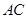与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F， EF⊥AC，连结AF、CE. 
、
相交于点O，村庄C的村民在公路的旁边建三个加工厂 A、B、D，已知AB=BC=CD=DA=5公里，村庄C到公路
，BC=
，DC=
，
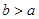，点M是AB边的中点．
