题目内容
如图，在Rt△ABC中，∠ABC= 90°，以AB为直径的⊙O与AC边交与点D．过D作⊙O的切线交BC与点E．连接OE.
(1)证明：OE∥AC；
(2)①当∠BAC= °时，四边形ODEB是正方形；
②当∠BAC= °时，AD=3DE.
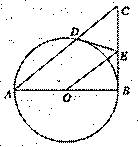
(1)连接OD∵DE是⊙O的切线，D是切点∴OD⊥DE
∴∠ODE=∠OBE= 90° ∵OD=OB,OE=OE ∴Rt△ODF≌Rt△OBE
∴∠DOE=∠EOB ∵∠A=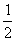
∠BOD ∴∠A=∠EOE
∴OE∥AC……5分 (2)①45，……7分②30…………9分
练习册系列答案
一本好题口算题卡系列答案
相关题目
上一点（不与A，B重合），连接CP，过点P作PQ⊥CP交AD边于点Q，连接CQ．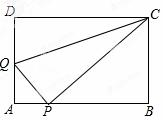
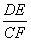= ．（用含m，n的代数式表示）
cm2 B. 
cm2 C. 6
cm2 D．3
．（只写出一个）．