题目内容
如图,抛物线y=ax2 +bx+c经过点A(-3,0)、C(0,4),点B在抛物线上,CB
∥X轴.且AB平分∠CAO.
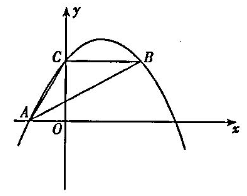
(1)求抛物线的解析式.
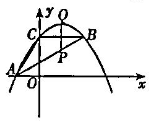
(2)线段AB上有一动点P,过P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,直接写出点M的坐标;如果不存在,说明理由,
解:(1)A(-3,0)、C(0,4),所以AC=5,OC=4.
∵AB平分∠CAO ∴∠CAB=∠BAO
∵CB∥x轴∴∠CBA=∠BAO
∴∠CAB=∠CBA
∴AC=BC=5
∴B(5,4)………………………………………1分
A(-3,0)、C(0,4)、B(5,4)代入y=ax2+bx+c得:
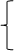 0= 9a-3b+c
0= 9a-3b+c
4=c ………………………………………2分
4=25a+5b+c
解得:a=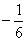 ,b=
,b= ,c=4.
,c=4.
所以y=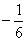 x2+
x2+ x+4……………………………3分
x+4……………………………3分
(2)设AB的解析式为:y=kx+b,……………4分
 把A(-3,0)、B(5,4)代入 0=-3k+b…………………5分
把A(-3,0)、B(5,4)代入 0=-3k+b…………………5分
4=5k+b
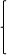 解得: k=
解得: k= .所以AB的解析式为y=
.所以AB的解析式为y= x+
x+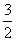 ;……………………6分
;……………………6分
B=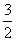 .
.
可设P(x, x+
x+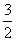 ),Q(x,
),Q(x,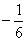 x2+
x2+ x+4),
x+4),
则PQ=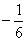 x2+
x2+ x+4-(
x+4-( x+
x+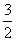 )=
)=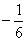 x2+
x2+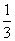 x+
x+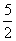 =
=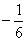 (x-1)2+
(x-1)2+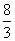 …………7分
…………7分
当x=1时,PQ最大,且最大值为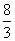 .…………8分
.…………8分
(3)存在.M的坐标为(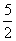 ,9)和(
,9)和(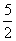 ,-11)…
,-11)…

练习册系列答案
相关题目
 的结果是( )
的结果是( )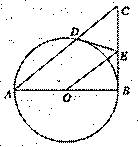

 的结果中二次项系数是( )
的结果中二次项系数是( ) ,若已知
,若已知 和
和 ,求
,求 =__________
=__________ A.点A与点B B.点A与点D
A.点A与点B B.点A与点D