题目内容
20.已知:(a+2b)y2-ya-1=3是关于y的一元一次方程.(1)求a、b的值;
(2)若x=a是方程$\frac{x+2}{6}$-$\frac{x-1}{2}$+3=x-$\frac{x-m}{3}$的解,求|a-b-2|-|b-m|的值.
分析 (1)根据一元一次方程的定义可得a-1=1,a+2b=0,解出a、b的值;
(2)把x=2代入方程$\frac{x+2}{6}$-$\frac{x-1}{2}$+3=x-$\frac{x-m}{3}$,解出m的值,然后再代入|a-b-2|-|b-m|求值即可.
解答 解:(1)由题意得:a-1=1,a+2b=0,
解得:a=2,b=-1;
(2)把x=a=2代入方程$\frac{x+2}{6}$-$\frac{x-1}{2}$+3=x-$\frac{x-m}{3}$得:
$\frac{4}{6}$-$\frac{1}{2}$+3=2-$\frac{2-m}{3}$,
解得:m=5.5,
当a=2,b=-1,m=5.5时,
|a-b-2|-|b-m|=|2+1-2|-|-1-5.5|=1-6.5=-5.5.
点评 此题主要考查了一元一次方程的定义,以及一元一次方程的解,绝对值,关键是掌握一元一次方程的定义:只含有一个未知数(元),且未知数的次数是1,这样的方程叫一元一次方程.

练习册系列答案
相关题目
8.下列各式中,正确的是( )
| A. | $\frac{-x+y}{-x-y}$=$\frac{x-y}{x+y}$ | B. | $\frac{-x+y}{x-y}$=$\frac{-x-y}{x-y}$ | C. | $\frac{-x+y}{-x-y}$=$\frac{x+y}{x-y}$ | D. | $\frac{-x+y}{x-y}$=$\frac{x-y}{x+y}$ |
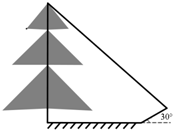 某同学测量一棵树的高度,某时刻树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为6米,坡面上的影长为4米,一直斜坡的坡角为30°,同一时刻,一根长为3米,垂直于地面放置的标杆在地面上的影长为1.5米,则树的高度为(14+4$\sqrt{3}$)米.
某同学测量一棵树的高度,某时刻树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为6米,坡面上的影长为4米,一直斜坡的坡角为30°,同一时刻,一根长为3米,垂直于地面放置的标杆在地面上的影长为1.5米,则树的高度为(14+4$\sqrt{3}$)米.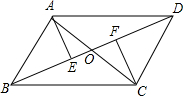 如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,则图中的全等三角形有△AOE≌△COF,Rt△ABE≌Rt△CDF,△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB.
如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,则图中的全等三角形有△AOE≌△COF,Rt△ABE≌Rt△CDF,△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB.