题目内容
4.已知a与b互为相反数,c与d互为倒数,m的绝对值为2,求式子$\frac{a+b}{m}$-cd+m的值.分析 根据题意可知a+b=0,cd=1,m=±2,然后代入计算即可.
解答 解:∵a与b互为相反数,
∴a+b=0.
∵c与d互为倒数,
∴cd=1.
∵m的绝对值为2,
∴m=±2.
当m=2时,原式=0-1+2=1;
当m=-2时,原式=0-1-3=-3.
∴式子$\frac{a+b}{m}$-cd+m的值为1或-3.
点评 本题主要考查的是求代数式的值,根据相反数、倒数和绝对值的定义求得a+b=0,cd=1,m=±2是解题的关键.

练习册系列答案
相关题目
14.若向量$\overrightarrow{a}$与$\overrightarrow{b}$均为单位向量,则下列结论中正确的是( )
| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | $\overrightarrow{a}$=-$\overrightarrow{b}$ | C. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D. | $\overrightarrow{a}$=1 |
9.下面两个圈分别表示负数集和分数集,请把下列6个数填入这两个圈中合适的位置.
-15%,-(-$\frac{3}{7}$),-2015,3.14,-(+9),-0.$\stackrel{•}{1}$.
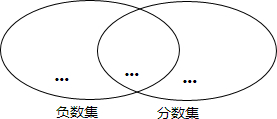
-15%,-(-$\frac{3}{7}$),-2015,3.14,-(+9),-0.$\stackrel{•}{1}$.

14.如果一个多边形的每个内角都是120°,那么这个多边形是( )
| A. | 三角形 | B. | 六边形 | C. | 七边形 | D. | 九边形 |
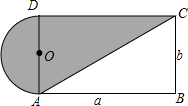 设计一个商标图案(如图阴影部分),其中O为半圆的圆心,AB=a,BC=b,
设计一个商标图案(如图阴影部分),其中O为半圆的圆心,AB=a,BC=b,