题目内容
6．如图，按图中结构规律的第20个图形中三角形的个数是（ ）
| A． | 75个 | B． | 77个 | C． | 79 个 | D． | 81个 |
分析 观察图形得到第1个图形的三角形的个数为1，第2个图形的三角形的个数为1+4=5，第3个图形的三角形的个数为1+4×2=9，第4个图形的三角形的个数为1+4×3=13，…，则可得到第n个图形的三角形的个数为1+4×（n-1），然后把n=20代入计算即可．
解答 解：∵第1个图形的三角形的个数为1，
第2个图形的三角形的个数为1+4×1=5，
第3个图形的三角形的个数为1+4×2=9，
第4个图形的三角形的个数为1+4×3=13，
…
∴第20个图形的三角形的个数为1+4×19=77．
故选：B．
点评 此题考查图形的变化规律，找出图形变化的规律，得出数字规律是解题关键．
练习册系列答案
相关题目
（本题满分10分）
一汽车租赁公司拥有某种型号的汽车100辆．公司在经营中发现每辆车的月租金
x(元)与每月租出的车辆数(y)有如下关系：
x | 4500 | 4000 | 3800 | 3200 |
y | 70 | 80 | 84 | 96 |
（1）观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y（辆）与每辆车的月租金x（元）之间的关系式.
（2）已知租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元． 每辆车的月租金定为多少元时，才能使公司获得最大月收益？请求出公司的最大月收益是多少元．
1．设二次函数y1=a（x-m）（x-n）（a≠0，m≠n）的图象与一次函数y2=dx+e（d≠0）的图象交于点（m，0），若函数y=y2+y1的图象与x轴仅有一个交点，则（ ）
| A． | a（m-n）=d | B． | a（n-m）=d | C． | a（m-n）2=d | D． | a（m+n）2=d |
11．温度上升-3摄氏度后，又下降3摄氏度，实际是（ ）
| A． | 上升1℃ | B． | 上升6℃ | C． | 下降6℃ | D． | 不变 |
18．
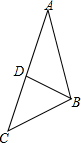如图，在△ABC中，D是边AC上一点，连接BD，给出下列条件：①∠ABD=∠ACB；②AB2=AD•AC；③∠A=∠ABD；④AB•BC=AC•BD．其中单独能够判定△ABD∽△ACB的个数是（ ）
如图，在△ABC中，D是边AC上一点，连接BD，给出下列条件：①∠ABD=∠ACB；②AB2=AD•AC；③∠A=∠ABD；④AB•BC=AC•BD．其中单独能够判定△ABD∽△ACB的个数是（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
15．下面四组图形中，必是相似三角形的为（ ）
| A． | 有一个角为40°的两个等腰三角形 | |
| B． | 两个直角三角形 | |
| C． | 两条边对应成比例，一个对应角相等的两个三角形 | |
| D． | 有一个角为100°的两个等腰三角形 |