题目内容
18. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2.
其中,正确结论的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①由二次函数y=ax2+bx+c与x轴有2个交点,可得b2-4ac>0;
②由抛物线开口方向、对称轴、抛物线与y轴的交点,可判定a,b,c的符号,继而判定abc<0;
③由关于x的一元二次方程ax2+bx+c-m=0没有实数根,可得直线y=m与抛物线无交点,继而求得答案.
解答 解:①∵二次函数y=ax2+bx+c与x轴有2个交点,
∴b2-4ac>0;故正确;
②∵开口向下,
∴a<0,
∵对称轴在y轴右侧,
∴b>0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,故正确;
③∵关于x的一元二次方程ax2+bx+c-m=0没有实数根,
∴即直线y=m与抛物线无交点,
∴m>2,故正确.
故选D.
点评 此题考查了二次函数的图象与系数的关系.注意二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点以及抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
9.下列图形绕某点旋转180°后,不能与原来图形重合的是( )
| A. |  | B. |  | C. |  | D. |  |
6.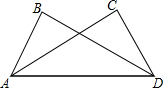 如图,在△ADB和△ADC中,有以下条件:①BD=AC,AB=DC;②∠B=∠C,∠BAD=∠CDA;③∠B=∠C,BD=AC;④∠ADB=∠CAD,BD=AC.其中能得出△ADB≌△ADC的是( )
如图,在△ADB和△ADC中,有以下条件:①BD=AC,AB=DC;②∠B=∠C,∠BAD=∠CDA;③∠B=∠C,BD=AC;④∠ADB=∠CAD,BD=AC.其中能得出△ADB≌△ADC的是( )
 如图,在△ADB和△ADC中,有以下条件:①BD=AC,AB=DC;②∠B=∠C,∠BAD=∠CDA;③∠B=∠C,BD=AC;④∠ADB=∠CAD,BD=AC.其中能得出△ADB≌△ADC的是( )
如图,在△ADB和△ADC中,有以下条件:①BD=AC,AB=DC;②∠B=∠C,∠BAD=∠CDA;③∠B=∠C,BD=AC;④∠ADB=∠CAD,BD=AC.其中能得出△ADB≌△ADC的是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
13. 如图,∠1=( )
如图,∠1=( )
 如图,∠1=( )
如图,∠1=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |