题目内容
10.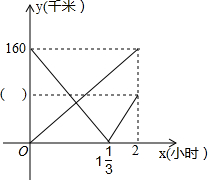 甲乙两地相距240千米,一辆货车从甲地出发驶往乙地,货车行驶一段时间后,一辆轿车从乙地出发驶往甲地,两车与途中一服务区的距离y(千米)与轿车出发时间x(小时)之间的函数关系如图所示:
甲乙两地相距240千米,一辆货车从甲地出发驶往乙地,货车行驶一段时间后,一辆轿车从乙地出发驶往甲地,两车与途中一服务区的距离y(千米)与轿车出发时间x(小时)之间的函数关系如图所示:(1)求货车和轿车的速度;
(2)补全图中( )中的内容,求轿车与途中服务区的距离y(千米)与轿车出发时间x(小时)之间的函数关系;
(3)求货车出发多长时间后两车相遇.
分析 (1)由图可知当轿车出发时,货车恰好离开服务区,货车2小时行驶的路程为160km,轿车1$\frac{1}{3}$小时行驶的路程为160km,根据速度=路程÷时间,即可解答;
(2)由轿车的速度为120km/h,所以2小时轿车行驶的路程为120×2=240km,则240-160=80,故( )中填80;利用待定系数法求函数解析式,分两种情况:当0≤x<1$\frac{1}{3}$时,当x>1$\frac{1}{3}$时.
(3)当两车相遇时,两车行驶的路程之和为240km,轿车出发前货车行驶的路程为:240-160=80km,则货车比轿车早出发时间为:80÷80=1(h),
设货车出发后t小时相遇,则依据题意得:80t+120(t-1)=240,即可解答.
解答 解:(1)由图可知当轿车出发时,货车恰好离开服务区,货车2小时行驶的路程为160km,轿车1$\frac{1}{3}$小时行驶的路程为160km,
则可得,货车的速度为:160÷2=80(km/h),轿车的速度为:160÷1$\frac{1}{3}$=120(km/h).
(2)∵轿车的速度为120km/h,
∴2小时轿车行驶的路程为120×2=240km,
∴240-160=80,
故( )中填80;
设当0≤x<1$\frac{1}{3}$时,y与x的函数关系式为y=k1x+b1,
把(0,160),($\frac{4}{3}$,0)带入可得:$\left\{\begin{array}{l}{{b}_{1}=160}\\{\frac{4}{3}{k}_{1}+{b}_{1}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-120}\\{{b}_{1}=160}\end{array}\right.$
∴y=-120x+160.
当x>1$\frac{1}{3}$时,y与x的函数关系式为y=k2x+b2,
把($\frac{4}{3}$,0),(2,80)代入可得:$\left\{\begin{array}{l}{\frac{4}{3}{k}_{2}+{b}_{2}=0}\\{2{k}_{2}+{b}_{2}=80}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=120}\\{{b}_{2}=-160}\end{array}\right.$
∴y=120x-160.
(3)当两车相遇时,两车行驶的路程之和为240km,
轿车出发前货车行驶的路程为:240-160=80km,
则货车比轿车早出发时间为:80÷80=1(h),
设货车出发后t小时相遇,
则依据题意得:80t+120(t-1)=240,
解得:t=1.8(h).
点评 本题考查了一次函数的应用,从图中准确获取信息求出两人的速度是解题的关键,易错点在于要分两种情况求解.

| A. | 30°,60°,90° | B. | 60°,120°,180° | C. | 40°,80°,120° | D. | 50°,100°,150° |
| A. |  | B. |  | C. |  | D. |  |
 如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动0,2,6,8秒时,△DEB与△BCA全等.
如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动0,2,6,8秒时,△DEB与△BCA全等.