题目内容
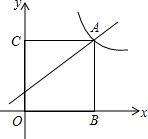 如图,在平面直角坐标系中,一次函数y=kx+1的图象与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+1的图象与反比例函数y=| 9 |
| x |
(1)求一次函数的关系式;
(2)一次函数图象与x轴的交点为D,求△ABD的面积.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)利用正方形的性质可设A(t,t)(t>0),再把A(t,t)代入y=
求出t的值,得到A点坐标,然后把A点坐标代入y=kx+1可计算出k,从而得到一次函数解析式;
(2)先确定D点坐标,然后根据三角形面积公式求解.
| 9 |
| x |
(2)先确定D点坐标,然后根据三角形面积公式求解.
解答:解:(1)∵四边形OBAC是正方形,
∴AB=AC,
设A(t,t)(t>0),
把A(t,t)代入y=
得t2=9,解得t=3或t=-3(舍去),
∴把A(3,3)代入y=kx+1得3k+1=3,解得k=
,
∴一次函数解析式为y=
x+1;
(2)当y=0时,
x+1=0,解得x=-
,
∴D(-
,0),
∴△ABD的面积=
•(3+
)•3=
.

∴AB=AC,
设A(t,t)(t>0),
把A(t,t)代入y=
| 9 |
| x |
∴把A(3,3)代入y=kx+1得3k+1=3,解得k=
| 2 |
| 3 |
∴一次函数解析式为y=
| 2 |
| 3 |
(2)当y=0时,
| 2 |
| 3 |
| 3 |
| 2 |
∴D(-
| 3 |
| 2 |
∴△ABD的面积=
| 1 |
| 2 |
| 3 |
| 2 |
| 27 |
| 4 |
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
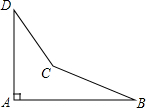 一个飞机零件的形状如图所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,李师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?
一个飞机零件的形状如图所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,李师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗? 王师傅驾车到某地,汽车出发前油箱有油50升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
王师傅驾车到某地,汽车出发前油箱有油50升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.