Question

如图，点A在y轴上，点B在x轴上，以AB为边作正方形ABCD，P为正方形ABCD的对称中心，正方形ABCD的边长为

10

，tan∠ABO=3．
（1）分别写出A，C，P三点的坐标．
（2）经过坐标原点O且顶点为P的抛物线是否经过C点，请说明理由．

Answer 1

考点：正方形的性质,二次函数图象上点的坐标特征,全等三角形的判定与性质

专题：

分析：（1）如图，作辅助线；求出AO、BO的长度；证明△ABO≌△BCQ，得到BQ=AO=3，CQ=BO=1，即可解决问题．
（2）求出抛物线解析式，检验该抛物线是否经过点C，即可解决问题．

解答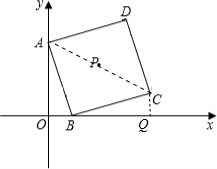：解：（1）如图，连接AC；过点C作CQ⊥x轴于点Q；
∵tan∠ABO=3，
∴AO：BO=1：3，设AO=3λ，
则BO=λ；而AB=

10

，∠AOB=90°，
∴9λ²+λ²=10，
解得：λ=1，AO=3，BO=1；
∵ABCD是正方形，
∴AB=BC，∠ABC=90°；
∵∠AOB=∠BQC=90°，
∴∠OAB+∠ABO=∠ABO+∠CBQ，
∴∠OAB=∠CBQ；
在△ABO与△BCQ中，

∠OAB=∠CBQ ∠AOB=∠BQC AB=BC

，
∴△ABO≌△BCQ（AAS），
∴BQ=AO=3，CQ=BO=1；
∴OQ=4；A（0，3）、C（4，1）；
设P（m，n）．
∵P为线段AC的中点，
∴m=

0+4

2

=2，n=

3+1

2

=2，
∴P（2，2）；
∴A，C，P三点的坐标分别为（0，3）、（4，1）、（2，2）．
（2）设抛物线的解析式为y=a（x-2）²+2，
由题意得：4a+2=0，
解得：a=-

1

2

，
∴y=-

1

2

(x-2)2+2；
∵当x=4时，y=0，
∴该抛物线不经过点C（4，1）．

点评：该题主要考查了正方形的性质、全等三角形的判定、抛物线上点的坐标特征等知识点及其应用问题；解题的关键是作辅助线，构造全等三角形．