题目内容
如图所示，在矩形ABCD中，BD=10，△ABD的内切圆半径为2，切三边于E、F、G，则矩形两边AB=分析：根据勾股定理，得AB2+AD2=100①；再根据直角三角形的内切圆的半径等于两条直角边的和与斜边的差的一半，得AB+AD=14②．联立两式可求得AB、AD的长．
解答：解：Rt△ABD中，BD=10，由勾股定理，得：
AB2+AD2=AB2=100…①；
设△ABD内切圆的半径为R，则有：
R=
=2，即AB+AD=14…②；
联立①②得：
，解得
．
故AB的长为6，AD的长为8．
AB2+AD2=AB2=100…①；
设△ABD内切圆的半径为R，则有：
R=
| AB+AD-BD |
| 2 |
联立①②得：
|
|
故AB的长为6，AD的长为8．
点评：本题主要考查直角三角形的性质、勾股定理、直角三角形内切圆半径的计算方法等知识点．
练习册系列答案
相关题目
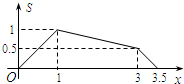
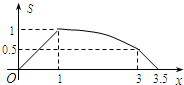
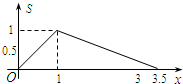
如图所示，在矩形ABCD中，AB=1，BC=2，E是CD边的中点．点P从点A开始，沿逆时针方向在矩形边上匀速运动，到点E停止．设点P经过的路程为x，△APE的面积为S，则S关于x的函数关系的大致图象是（ ）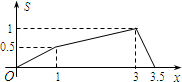
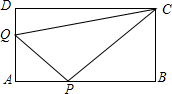P也随之停止运动．用t表示移动时间，设四边形QAPC的面积为S．
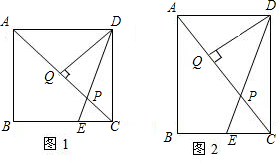B=nBC
如图所示，在矩形ABCD中，AB=4cm，BC=8cm、点P从点D出发向点A运动，同时点Q从点B出发向点C运动，点P、Q的速度都是1cm/s．