题目内容
6．
如图，已知⊙O的半径为2，∠A=30°与圆交于B、C两点，求阴影部分的面积．
分析 连接OC、OB，可得∠AOB=60°，且△BOC是边长为2的等边三角形，再根据弓形面积=扇形面积-等边三角形面积即可得．
解答 解：如图，连接OC、OB，
∵∠A=30°，
∴∠AOB=60°，
∵半径为2，
∴△BOC是边长为2的等边三角形，
则阴影部分的面积为$\frac{60°•π•{2}^{2}}{360°}$-$\frac{\sqrt{3}}{4}$×22=$\frac{2}{3}$π-$\sqrt{3}$．
点评 本题主要考查扇形面积的计算，同时还考查了圆周角定理和等边三角形面积的计算，掌握圆中不规则图形的面积计算方法是解题的关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
如图所示，在△ABC中，∠A=60°，BD，CE是两条高，求证：△ADE∽△ABC．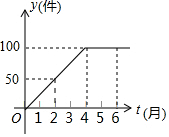
如图是某工厂在2014年前6个月生产某产品的总产量y（件）和时间t（月）的关系的图象，根据图象回答下列问题：