题目内容
2．有一枚均匀的正方体骰子，骰子各个面上的点数分别为1，2，3，4，5，6，若任意抛掷一次骰子，朝上面的点数恰为2的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
分析 根据概率公式即可得．
解答 解：∵任意抛掷一次骰子共有6种等可能结果，其中朝上面的点数恰为2的只有1种，
∴朝上面的点数恰为2的概率是$\frac{1}{6}$，
故选：A．
点评 本题主要考查概率公式，掌握随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数是解题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
12．
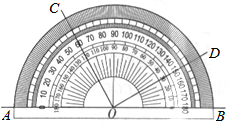如图所示，用量角器度量一些角的度数．下列结论中正确的是（ ）
如图所示，用量角器度量一些角的度数．下列结论中正确的是（ ）| A． | ∠BOC=60° | B． | ∠COD=150° | ||
| C． | ∠AOC与∠BOD的大小相等 | D． | ∠AOC与∠BOD互余 |
13．
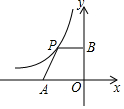如图，平面直角坐标系中，点A是x轴负半轴上一个定点，点P是函数y=$\frac{-6}{x}$（x＜0）上一个动点，PB⊥y轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会（ ）
如图，平面直角坐标系中，点A是x轴负半轴上一个定点，点P是函数y=$\frac{-6}{x}$（x＜0）上一个动点，PB⊥y轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会（ ）| A． | 先增后减 | B． | 先减后增 | C． | 逐渐减小 | D． | 逐渐增大 |
10．下面四个等式的变形中正确的是（ ）
| A． | 由4x+8=0得x+2=0 | B． | 由x+7=5-3x得4x=2 | ||
| C． | 由$\frac{3}{5}$x=4得x=$\frac{12}{5}$ | D． | 由-4（x-1）=-2得4x=-6 |
14．下列说法正确的是（ ）
| A． | -x2y-22x3y是六次多项式 | B． | $\frac{3x+y}{3}$是单项式 | ||
| C． | -$\frac{1}{2}$πab的系数是-$\frac{1}{2}$π，次数是2次 | D． | $\frac{1}{a}$+1是多项式 |
如图是人民广场内的一个矩形花园，花园的长为100米，宽为50米，在它的四角各建一个同样大小的正方形休闲区，四周建有与观光休息亭等宽的观光大道，其余部分（图内阴影部分）种植的是不同花草．已知种植花草部分的面积为3600米2，那么花园各角处的正方形休闲区的边长多少米．