题目内容
15.观察下列各式:$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}-\sqrt{2}$,$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$…请利用你发现的规律计算:($\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{2+\sqrt{3}}$+$\frac{1}{\sqrt{5}+2}$+…+$\frac{1}{\sqrt{2016}+\sqrt{2015}}$)×($\sqrt{2016}$+$\sqrt{2}$)=2014.
分析 原式第一个因式中各项分母有理化后,再利用平方差公式计算即可得到结果.
解答 解:原式=($\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$+$\sqrt{5}$-2+…+$\sqrt{2016}$-$\sqrt{2015}$)×($\sqrt{2016}$+$\sqrt{2}$)=($\sqrt{2016}$-$\sqrt{2}$)×($\sqrt{2016}$+$\sqrt{2}$)=2016-2=2014,
故答案为:2014
点评 此题考查了分母有理化,二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
相关题目
3.下列命题是真命题的是( )
| A. | 如果a2=b2,则a=b | |
| B. | 两边一角对应相等的两个三角形全等 | |
| C. | $\sqrt{81}$的算术平方根是9 | |
| D. | x=2,y=1是方程2x-y=3的解 |
20.下列各式中属于最简二次根式的是( )
| A. | $\sqrt{{x}^{2}y}$ | B. | $\sqrt{24}$ | C. | $\sqrt{{x}^{2}+1}$ | D. | $\sqrt{0.5}$ |
5.下列事件中不是随机事件的是( )
| A. | 打开电视机正好在播放广告 | |
| B. | 从有黑球和白球的盒子里任意拿出一个正好是白球 | |
| C. | 从课本中任意拿一本书正好拿到数学书 | |
| D. | 明天太阳会从西方升起 |
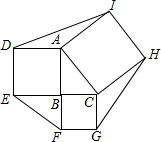 图,已知Rt△ABC,∠ABC=90°,AB=4,BC=3,以三边为边长作正方形,则所得的六边形DEFGHI的面积为74.
图,已知Rt△ABC,∠ABC=90°,AB=4,BC=3,以三边为边长作正方形,则所得的六边形DEFGHI的面积为74. 如图,C为线段AB上一点,AD∥EB,AC=BE,AD=BC.求证:△ACD≌△BEC.
如图,C为线段AB上一点,AD∥EB,AC=BE,AD=BC.求证:△ACD≌△BEC.