题目内容
11. 如图,在正方形ABCD中,CE⊥DF,求证:CE=DF.
如图,在正方形ABCD中,CE⊥DF,求证:CE=DF.
分析 由在正方形ABCD中,CE⊥DF,易证得△BCE≌△CDF(ASA),即可证明.
解答 证明:∵四边形ABCD是正方形,
∴BC=CD,∠B=∠DCF=90°,
∴∠BCE+∠DCE=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=90°,
∴∠BCE=∠CDF,
在△BCE和△CDF中,
$\left\{\begin{array}{l}{∠B=∠DCF}\\{BC=CD}\\{∠BCE=∠CDF}\end{array}\right.$,
∴△BCE≌△CDF(ASA),
∴DF=CE.
点评 此题考查了正方形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.如图是小李书桌上放的一本书,则这本书的俯视图是( )


| A. |  | B. |  | C. |  | D. |  |
6.下列分式中,为最简分式的是( )
| A. | $\frac{a+3}{{a}^{2}+3}$ | B. | $\frac{a+b}{{a}^{2}-{b}^{2}}$ | C. | $\frac{12}{3x-3y}$ | D. | $\frac{x}{xy}$ |
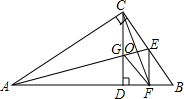 如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC,交BC于点E,CD⊥AB于点D,EF⊥AB于点F,CD交AE于点G,CF交AE于点O.求证:四边形CGFE是菱形.
如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC,交BC于点E,CD⊥AB于点D,EF⊥AB于点F,CD交AE于点G,CF交AE于点O.求证:四边形CGFE是菱形.