Question

已知：△ABC的顶点坐标分别是A（-4，2），B（2，4），C（-1，0），求△ABC的面积．（建立坐标系，在坐标系中画出△ABC）

Answer 1

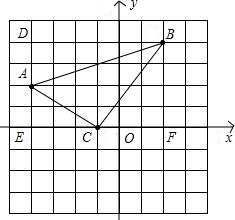解：由图可知△ABC所在的矩形是DEFB，
由A（-4，2），B（2，4），C（-1，0），可知DE=BF=4，DB=EF=6，AD=AE=2，CE=CF=3，
∴S_矩形DEFB=DE•EF=6×6=36，S_△ADB=DB•AD=×6×2=6，S_△ADB=CE•AE=×3×2=3，
S_△BCF=CF•BF=×3×4=6，
∴S_△AOB=S_矩形DEFB-S_△ADB-S_△ADB-S_△BCF=36-6-3-6=21．
分析：先根据题意画出图形，找出三角形所在的矩形BDEF，求出其面积，再减去多余的三角形的面积即可．
点评：本题考查的是三角形面积的求法，解答此类题目时要有整体思想，不要只局限于三角形的面积公式中而引起复杂的计算过程．