题目内容
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1。
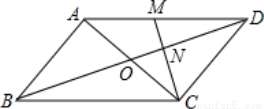
(1)求BD的长
(2)若△DCN的面积为2,求四边形ABNM的面积。
(1)6;(2)5.
【解析】
试题分析:(1)根据平行四边形的性质得AD∥BC,从而△MND∽△CNB,结合M为AD中点,可得BN=2DN,又OB=OD,ON=1,所以可求出BD=6;(2)利用△MND∽△CNB,得MN:CN=DN:BN=1:2,从而可得S△BNC=2S△CND=4,S△MND=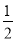 S△CND=1,所以S△ABD=S△BCD=6,然后根据S四边形ABNM=S△ABD- S△MND
S△CND=1,所以S△ABD=S△BCD=6,然后根据S四边形ABNM=S△ABD- S△MND
可解.
试题解析:解(1)∵平行四边形ABCD,∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC;∴△MND∽△CNB, 2分
∴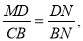 ∵M为AD中点,∴MD=
∵M为AD中点,∴MD=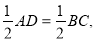
即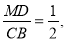 ∴
∴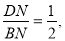 即BN=2DN, 4分
即BN=2DN, 4分
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1, 6分
∴x+1=2(x-1),解得:x=3 ∴BD=2x=6 8分
(2) ∵△MND∽△CNB,且相似比为1:2,∴MN:CN=DN:BN=1:2
∴S△MND=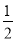 S△CND=1,S△BNC=2S△CND=4。 10分
S△CND=1,S△BNC=2S△CND=4。 10分
∴S△ABD=S△BCD= S△BCN+S△CND=4+2=6
∴S四边形ABNM=S△ABD- S△MND =6-1=5 12分
考点:1.平行四边形的性质;2.相似三角形的判定与性质.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
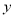 =f(x)=
=f(x)=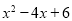 的图象向左平移1个单位,再向上平移1个单位,所得图象对
的图象向左平移1个单位,再向上平移1个单位,所得图象对
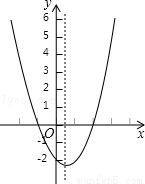

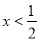 时,y随x的增大而减小
时,y随x的增大而减小 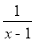 )÷
)÷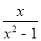 ,再选择一个恰当的x值代人并求值.
,再选择一个恰当的x值代人并求值.