题目内容
13.造一个方程,使它的根是方程3x2-7x+2=0的根;(1)大3;
(2)倒数.
分析 设方程3x2-7x+2=0的根为a和b,根据根与系数的关系得到a+b=$\frac{7}{3}$,ab=$\frac{2}{3}$,
(1)先计算出a+3+b+3和(a+3)(b+3)的值,然后根据根与系数的关系写出满足条件的一元二次方程;
(2)先计算出$\frac{1}{a}$+$\frac{1}{b}$和$\frac{1}{a}$•$\frac{1}{b}$的值,然后根据根与系数的关系写出满足条件的一元二次方程.
解答 解:设方程3x2-7x+2=0的根为a和b,
则a+b=$\frac{7}{3}$,ab=$\frac{2}{3}$,
(1)a+3+b+3=$\frac{7}{3}$+6=$\frac{25}{3}$,(a+3)(b+3)=ab+3(a+b)+9=$\frac{2}{3}$+7+9=$\frac{50}{3}$,
所以所求方程为x2-$\frac{25}{3}$x+$\frac{50}{3}$=0,即3x2-25x+50=0;
(2)$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{7}{2}$,$\frac{1}{a}$•$\frac{1}{b}$=$\frac{3}{2}$,
所以所求方程为x2-$\frac{7}{2}$x+$\frac{3}{2}$=0,即2x2-7x+3=0.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.也考查了根与系数的关系.

练习册系列答案
相关题目
4. 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )| A. | 873名 | B. | 1115名 | C. | 485名 | D. | 1067名 |
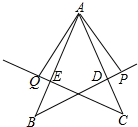 已知,如图,AB=AC,AD=AE,AP⊥BD,AQ⊥CE,垂足分别为P、Q,求证:AP=AQ.
已知,如图,AB=AC,AD=AE,AP⊥BD,AQ⊥CE,垂足分别为P、Q,求证:AP=AQ. 如图,一辆小汽车从小山脚下的A点直线行驶15分钟到达山顶的B点,已知小汽车的平均速度为40千米/时,小山的高度BC约为6000米,求小山的坡比.
如图,一辆小汽车从小山脚下的A点直线行驶15分钟到达山顶的B点,已知小汽车的平均速度为40千米/时,小山的高度BC约为6000米,求小山的坡比. 如图,在△ABC中,BC=4,AC=6,△ABC的高AD与BE的比是多少?
如图,在△ABC中,BC=4,AC=6,△ABC的高AD与BE的比是多少?