题目内容
某同学在学习过程中，遇到这样的问题：求A=48×(
+
+…+
)的整数部分．百思而不得其解，于是向老师求教．数学老师进行了深入浅出的讲解：观察算式中每个分母中减数都是4，且被减数都在递增；
先看一般情形：
=…=
(
-
)
再看特殊情形：
当a=3时，
(
-
)=
当a=4时，
(
-
)=
老师讲解到这里时，该同学说：“老师我知道怎么做了”
（1）请你通过化简，说明一般情形
(
-
)=
的正确性；
（2）请你完成该同学的解答．
| 1 |
| 32-4 |
| 1 |
| 42-4 |
| 1 |
| 1002-4 |
先看一般情形：
| 1 |
| a2-4 |
| 1 |
| 4 |
| 1 |
| a-2 |
| 1 |
| a+2 |
再看特殊情形：
当a=3时，
| 1 |
| 4 |
| 1 |
| a-2 |
| 1 |
| a+2 |
| 1 |
| a2-4 |
当a=4时，
| 1 |
| 4 |
| 1 |
| a-2 |
| 1 |
| a+2 |
| 1 |
| a2-4 |
老师讲解到这里时，该同学说：“老师我知道怎么做了”
（1）请你通过化简，说明一般情形
| 1 |
| 4 |
| 1 |
| a-2 |
| 1 |
| a+2 |
| 1 |
| a2-4 |
（2）请你完成该同学的解答．
分析：（1）根据整式的加减法则把分式进行化简即可；
（2）根据题中所给出的式子把原式进行化简，求出A最接近的整数即可．
（2）根据题中所给出的式子把原式进行化简，求出A最接近的整数即可．
解答：解：（1）∵左边=
×（
-
）
=
×
=
×
=
，
∴左边=右边，即原式成立；
（2）∵
=
（
-
），
∴A=48×
[（1+
+…+
）-（
+
+…+
）]
=12×（1+
+
+
-
-
-
-
）
=25-12×（
+
+
+
）
∵12×（
+
+
+
）＜14×
＜
，
∴A的整数部分是24．
| 1 |
| 4 |
| a+2 |
| (a+2)(a-2) |
| a-2 |
| (a+2)(a-2) |
=
| 1 |
| 4 |
| a+2-a+2 |
| (a+2)(a-2) |
=
| 1 |
| 4 |
| 4 |
| a2-4 |
=
| 1 |
| a2-4 |
∴左边=右边，即原式成立；
（2）∵
| 1 |
| a2-4 |
| 1 |
| 4 |
| 1 |
| a-2 |
| 1 |
| a+2 |
∴A=48×
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 98 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 102 |
=12×（1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 99 |
| 1 |
| 100 |
| 1 |
| 101 |
| 1 |
| 102 |
=25-12×（
| 1 |
| 99 |
| 1 |
| 100 |
| 1 |
| 101 |
| 1 |
| 102 |
∵12×（
| 1 |
| 99 |
| 1 |
| 100 |
| 1 |
| 101 |
| 1 |
| 102 |
| 4 |
| 99 |
| 1 |
| 2 |
∴A的整数部分是24．
点评：本题考查的是分式的加减法，根据题意找出规律是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
某学习小组学习《整式的乘除》这一章后，共同研究课题，用4个能够完全重合的长方形，长、宽分别为a、b拼成不同的图形．在研究过程中，一位同学用这4个长方形摆成了一个大正方形．如图，利用面积不同表示方法验证了下面一个等式，则这个等式是（ ）
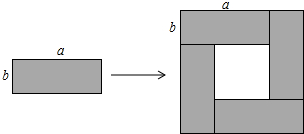
| A、a2-b2=（a+b）（a-b） | B、（a+b）2-（a-b）2=4ab | C、（a+b）2=a2+2ab+b2 | D、（a-b）2=a2-2ab+b2 |
的整数部分．百思而不得其解，于是向老师求教．数学老师进行了深入浅出的讲解：观察算式中每个分母中减数都是4，且被减数都在递增；
